- #1
CMJ96
- 50
- 0
Hello I have the following quantum circuit identity for converting a controlled U gate (4x4 matrix) into a series of CNOT gates and single qubit gates
$$ U= AXA^{\dagger}X$$
where A is a unitary matrix.
Here is a picture of the mentioned identity.
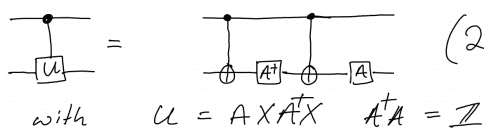
Can someone help me understand conceptually what is going on here? How do you actually define A?
$$ U= AXA^{\dagger}X$$
where A is a unitary matrix.
Here is a picture of the mentioned identity.
Can someone help me understand conceptually what is going on here? How do you actually define A?