Homotopy Class vs Fundamental Group.

[FallenApple]

They seem the same to me. So I can have many paths between a and b that are continuously deformable into each other while keeping the endpoints fixed. We say these function form a equivalence class [f]. This should be regardless if the endpoints are the same or not.

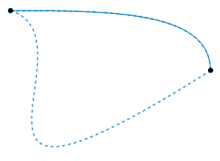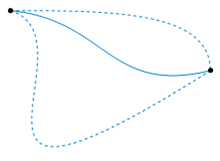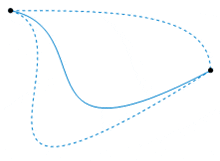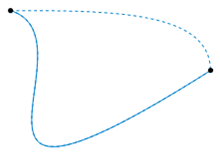
The fundamental group seems to be the same situation where the endpoints are the same. So why would they define it as all such [f]. That doesn't make too such sense. If I draw a bunch of lines between a and b, they are all homotopic to each other, and hence we would have one equalvalence class. [f]. How can we have a set? Could it be that there's a set [g] homotopic but not to elements in [f]? Would it be something like a path between a and b but with a self intersecting loop in between?

So the following image, source wiki, would it show one such subset of an equivalence class. One with no loops in between? So if I imagine a path inbetween those two points, where there is a self intersecting loop somewhere, then trying to warp it into one of the paths in the image seem like it would tear the curve by contracting an infinite amount of points into a cusp.

 

[andrewkirk]

If the range set in which the paths' images lie has a hole (eg consider the number plane with the origin removed) then there will be two homotopy classes, subdivided according to which side of the hole the path passes.

Whether a path crosses itself does not generally have any relation to whether it is the same homotopy class as another path.

The elements of the fundamental group are just the homotopy classes for the case where the start and end points are identical.

 

[FallenApple]

If the range set in which the paths' images lie has a hole (eg consider the number plane with the origin removed) then there will be two homotopy classes, subdivided according to which side of the hole the path passes.

Whether a path crosses itself does not generally have any relation to whether it is the same homotopy class as another path.

The elements of the fundamental group are just the homotopy classes for the case where the start and end points are identical.

That makes sense. Because the hole makes the path at the hole undefined. Essentially cutting the function.

So in the plane, with no holes, since self intersection is allowed, we have only one element in the group. Just one class. If there is a hole, we have two group elements, one of each subdivision. And we use classes as elements because just one class has an infinite amount of elements, and choosing different ones from the same class adds nothing qualitatively new.

 

[lavinia]

That makes sense. Because the hole makes the path at the hole undefined. Essentially cutting the function.

So in the plane, with no holes, since self intersection is allowed, we have only one element in the group. Just one class. If there is a hole, we have two group elements, one of each subdivision. And we use classes as elements because just one class has an infinite amount of elements, and choosing different ones from the same class adds nothing qualitatively new.

In the plane with a hole, this group is isomorphic to the integers. You have infinitely many elements, not two. Group elements are distinguished by the number of times they wind around the hole.

 

[FallenApple]

In the plane with a hole, this group is isomorphic to the integers. You have infinitely many elements, not two. Group elements are distinguished by the number of times they wind around the hole.

Oh, because we are considering the plane? Not just two points? So for two points, there are two classes, the set of paths on one side of the hole, and the set of classes on the other side of the hole. So it is like one is positive and the other is negative. But there are infinitely such pairs of points. So we have isomorphism to the integers.

But I don't see the winding argument though. Is it something like this image?

So there are two sets. One with a hole, and one without? Or is it a clockwise counter clockwise argument? So each loop is paired.

 

[lavinia]

Oh, because we are considering the plane? Not just two points? So for two points, there are two classes, the set of paths on one side of the hole, and the set of classes on the other side of the hole. So it is like one is positive and the other is negative. But there are infinitely such pairs of points. So we have isomorphism to the integers.

But I don't see the winding argument though. Is it something like this image?

So there are two sets. One with a hole, and one without? Or is it a clockwise counter clockwise argument? So each loop is paired.

I thought you meant the fundamental group. If you are not talking about loops then you don't have a group.

Still with two points, a curve starting at one of the points can wind around the hole some number of times before reaching the second point. This curve will not be homotopic to a curve that does not wind around the hole.

 

[andrewkirk]

@FallenApple Just adding to what @lavinia said: although there is no group structure, there will be a bijection between the homotopy classes and the integers, such that the paths in the homotopy class associated with integer n wind around the hole n times before reaching the end. If n is positive (negative) they wind clockwise (anticlockwise). [or maybe the convention works the other way - if there is a convention. I forget. ]