How can I find fixed points for a map with a range of r values?

[ggeo1]

Hello , i wanted to ask sth

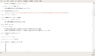
I have a map : x_n+1=rx_ne^-x_n , r>0 and r<20

I want to find fixed points .My problem is that i don't have a value or r.I can't manipulate the r values.

(if i had an r value i would do : r=2;)

My code is:

y[x_]:= r x Exp[-x];

To find the fixed points :

fp= Solve[y[x]-x==0 , x]

My output is:

Solve::ifun: Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information. >>

{{x -> 0}, {x -> Log[r]}}

The problem is that the answer is with values of r.

Any ideas?

 

[Evo]

Is "sth" supposed to mean something besides "somatotropin: a hormone produced by the anterior pituitary gland"? If it does, please type out the word you mean, this makes it possible for members (especially those who speak English as a second language) to undersatnd what you are saying.

 

[Simon_Tyler]

A fixed point is when x_n no longer changes, so
x_n+1=r x_ne^-x_n becomes
x = r x e^-x and if x is nonzero that leaves 1 = r e^-x.

This is solved to give x = log(r) (or x = 0 if it ever hits zero during its evaluation).

So x = log(r) and x = 0 are the only first order fixed points.
For r <= 1 the x=log(r) solution is unstable and the x=0 solution is stable. For r>1 the x=0 solution is unstable.

At about r=7.4 the x=log(r) becomes unstable and the system bifurcates.
The stable solutions are now solutions to x=e^{- x e-x(ex+r)} r² x.

Then you get the standard story of period doubling -> chaos -> period 3 -> doubling -> chaos -> etc...

You can generate a nice picture in Mathematica using something like

f=Compile[{{n,_Integer},{x0,_Real},{r,_Real}},Union[NestList[r # Exp[-#]&,x0,n][[-10;;-1]]]];
Show[{
  ListPlot[Flatten[Table[Thread[{r,f[1000,.01,r]}],{r,0,40,.01}],1],PlotStyle->PointSize[Tiny]],
  Plot[Log[r],{r,0,40},PlotStyle->Red]}]

To understand this better, you can read up about the canonical example:
http://en.wikipedia.org/wiki/Logistic_map

 

[ggeo1]

First of all , thank you very much for your complete information!

I am beginner in mathematica , so i can't undestand the code you send me.

My code is :

y[x_] := r x Exp[-x];
(* Find the fixed points*)

fp = NSolve[y[x] - x == 0, 
   x]; (* Here is the problem that i can't "insert" r somehow*)

Print ["Fixed points are " , fp];
(* Find the stability points*)
(* k is the stability index , if k>0 \unstable ,if k<0 stable*)

(* \[Lambda] is the stability index , if |\[Lambda]|<1 linear \stability ,if |\[Lambda]|>1 linear instability,if |\[Lambda]|=1 \
parabolic stability*)

\[Lambda][x_] = D[y[x], x]
x1 = x /. fp[[1]]; x2 = x /. fp[[2]];
Print [ "The first fixed point is " , x1 ,   "Stability index \[Lambda] = ", \[Lambda][x1]];
Print [ "The second fixed point is " , x2 ,  "Stability index \[Lambda] = ", \[Lambda][x2]];

If you know how can i insert 0<r<20 in my function with this kind of code..Unfortunately i can't do "fp = NSolve[y[x] - x == 0, x , {r,0,20} ]"

 

[Simon_Tyler]

I think you need to really think about what you want Mathematica to do for you.
For finding the stability indices, you probably want to stay symbolic the whole time.

I've attached a notebook that should do everything you want. Here's a screen shot of it:

 

[ggeo1]

Thank you very much!
I am studying it right now.

I used y[x_,r_]:=r x Exp[-x]
but then i did a mistake i think at Solve[y[x, r] == x, x]

But i would have not think the

Solve[(1 - Log[r])^2 == 1, r]

!

Thanks again!
You were very helpful and understanding.

 

[ggeo1]

Hello,

I have only one question for the fixed point x=1-Log[r].
If 1-logr<1 =>-logr<0 => logr>0 => r>1 then the point is stable.
Until here ,ok.

Why you are trying to solve (1-logr)^2=1 ?
(You are trying to find the limit of r value for the equation to be stable,but i can't figure the way)

As for the bifurcation diagram i did it with iterations with "while" and "if" commands and as i can see its the same.

Thanks!

 

[cenit]

You can generate a nice picture in Mathematica using something like

f=Compile[{{n,_Integer},{x0,_Real},{r,_Real}},Union[NestList[r # Exp[-#]&,x0,n][[-10;;-1]]]];
Show[{
  ListPlot[Flatten[Table[Thread[{r,f[1000,.01,r]}],{r,0,40,.01}],1],PlotStyle->PointSize[Tiny]],
  Plot[Log[r],{r,0,40},PlotStyle->Red]}]

Sorry for asking in this old thread, but my problems are related to this code which I'm trying to learn.
What's the meaning of the [[-10;;-1]] span? I really cannot understand it, and breaking the function in smaller parts doesn't help...

 

[Simon_Tyler]

Hi cenit, not a problem.

[[]] is an abreviation for http://reference.wolfram.com/mathematica/ref/Part.html" , and as explained in the documentation, negative integers reference a position from the end.

Assume you have a list called L. Then
L[[1]] gives the first element.
L[[1;;5]] gives the first 5 elements.
L[[1;;7;;2]] gives the elements 1,3,5,7.
L[[-1]] gives the last element
L[[-10,-1]] gives the last 10 elements.

I did this in the definition of the function f, this since we need the recursion to stabilize onto the attractive solutions - thus we keep the last 10 points and throw away the "junk" that came before. There are probably more smart and more efficient ways to do this, but for a quick forums solution, it was enough.

 

[cenit]

Hi cenit, not a problem.

[[]] is an abreviation for http://reference.wolfram.com/mathematica/ref/Part.html" , and as explained in the documentation, negative integers reference a position from the end.

Assume you have a list called L. Then
L[[1]] gives the first element.
L[[1;;5]] gives the first 5 elements.
L[[1;;7;;2]] gives the elements 1,3,5,7.
L[[-1]] gives the last element
L[[-10,-1]] gives the last 10 elements.

I did this in the definition of the function f, this since we need the recursion to stabilize onto the attractive solutions - thus we keep the last 10 points and throw away the "junk" that came before. There are probably more smart and more efficient ways to do this, but for a quick forums solution, it was enough.

thanks a lot. I missed the negative integers explanation somehow, even if I was looking for it...