- #1
Mkbul
- 14
- 0
Hello forum. Panhellenic exams begin in less than 10 days and stress is slowly but steadily been overtaking me these last few months. I've been solving problems out of a physics book, and i got stuck in one which involves mechanical oscillations (spring-mass system).
1. Homework Statement
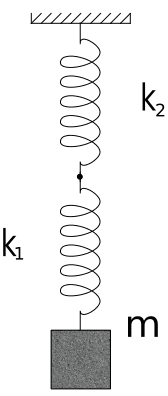
A small body of mass m is at rest hanging by ideal massless spring k1. Another ideal massless spring, k2, is tied to k1, and is hanging by the immovable ceiling. At some point, we move the body downwards by a distance d and at t=0 we let it move freely. Prove that the two springs act as a simple harmonic oscillator and calculate the constant of the restoring elastic force.
∑F = -kx = -mω2x
The usual method of tackling this kind of question is to take the spring-mass system in it's state of equillibrium, end up with an equation and then take the body in a random location during the oscillation and express ∑F in the form -kx with the help of the equation found. However, in this case, with the two springs, we have two forces from the springs, and their reactions (say F1 from the k1 spring and F2 for the k2 spring.). In the equillibrium, F1 is applied to the body and the edge of the k1 spring. The k2 spring is pulling the k1 spring upward and the reaction is forcing the immovable ceiling downwards (not that it's important for the solution).
Since with the help of jbriqqs444 i solved the problem, i figured i should edit with the solution so people can see it if they are interested:
4. The Solution:
For the body:
∑F=0 ⇔ F1=Wm ⇔ k1Δl=mg
Where Δl is the distance from where the spring wants to be.
Since the net force on the point the two springs intersect is zero, we can find, by equating the two spring forces, the different extents. So, at the meeting point:
∑F=0 ⇔ F1=F2 ⇔ k1Δl1=k2Δl2. But we already know that: k1Δl1=mg. So we got those two equations now.
We can also say that the total extent of both springs is: Δl=Δl1+Δl2⇔Δl=F1/k1+F2/k2⇔F1=[(k1k2)/(k1+k2)]Δl.
Which means that for the mass: ∑F=0⇔[(k1k2)/(k1+k2)]Δl=mg
Suppose we now take the system in a random location, and let's choose as the positive direction the direction of dislocation x. Then for the body:
∑F=-[(k1k2)/(k1+k2)](Δl+x)+mg=-(k1k2)/(k1+k2)Δl - [(k1k2)/(k1+k2)]x+mg = -[(k1k2)/(k1+k2)]x
That's what we wanted to prove. The body is doing simple harmonic oscillations with K=[(k1k2)/(k1+k2)]
I am really sorry if some of the terms i use are wrong. In Greece we use different notation and different expressions for physics problems. Thanks a million for any replies.
1. Homework Statement
A small body of mass m is at rest hanging by ideal massless spring k1. Another ideal massless spring, k2, is tied to k1, and is hanging by the immovable ceiling. At some point, we move the body downwards by a distance d and at t=0 we let it move freely. Prove that the two springs act as a simple harmonic oscillator and calculate the constant of the restoring elastic force.
Homework Equations
:[/B]∑F = -kx = -mω2x
The Attempt at a Solution
The usual method of tackling this kind of question is to take the spring-mass system in it's state of equillibrium, end up with an equation and then take the body in a random location during the oscillation and express ∑F in the form -kx with the help of the equation found. However, in this case, with the two springs, we have two forces from the springs, and their reactions (say F1 from the k1 spring and F2 for the k2 spring.). In the equillibrium, F1 is applied to the body and the edge of the k1 spring. The k2 spring is pulling the k1 spring upward and the reaction is forcing the immovable ceiling downwards (not that it's important for the solution).
Since with the help of jbriqqs444 i solved the problem, i figured i should edit with the solution so people can see it if they are interested:
4. The Solution:
For the body:
∑F=0 ⇔ F1=Wm ⇔ k1Δl=mg
Where Δl is the distance from where the spring wants to be.
Since the net force on the point the two springs intersect is zero, we can find, by equating the two spring forces, the different extents. So, at the meeting point:
∑F=0 ⇔ F1=F2 ⇔ k1Δl1=k2Δl2. But we already know that: k1Δl1=mg. So we got those two equations now.
We can also say that the total extent of both springs is: Δl=Δl1+Δl2⇔Δl=F1/k1+F2/k2⇔F1=[(k1k2)/(k1+k2)]Δl.
Which means that for the mass: ∑F=0⇔[(k1k2)/(k1+k2)]Δl=mg
Suppose we now take the system in a random location, and let's choose as the positive direction the direction of dislocation x. Then for the body:
∑F=-[(k1k2)/(k1+k2)](Δl+x)+mg=-(k1k2)/(k1+k2)Δl - [(k1k2)/(k1+k2)]x+mg = -[(k1k2)/(k1+k2)]x
That's what we wanted to prove. The body is doing simple harmonic oscillations with K=[(k1k2)/(k1+k2)]
I am really sorry if some of the terms i use are wrong. In Greece we use different notation and different expressions for physics problems. Thanks a million for any replies.
Last edited: