How to solve simple 2D space-time PDE numerically

[tworitdash]

I have a 2D space-time PDE and I want to solve it numerically over the time axis. The time initial field is already known with respect to space, i.e., the spatial distribution is already known at time `t = 0`. I solved the same PDF in Mathematica and got a solution. I tried to solve it numerically step wise in time and implemented the same numerical update equation in MATLAB. Both give me different results. I checked the paper where I took the question from and with only a visual inspection it feels like the one from Mathematica is more accurate. As time progresses, the numerical model becomes more erroneous.

The PDE:$$ \frac{\partial \eta(x, t)}{\partial t} + \sin\Big(\frac{2 \pi x}{L}\Big) \frac{\partial \eta(x, t)}{\partial x} = 0 $$

Boundary conditions: At the spatial boundaries, the function has a value of `0`.$$ \eta(0, t) = 0, \eta(L, t) = 0 $$The time initial field is given by

$$ \eta(x, 0) = \sin\Big(\frac{2 \pi x}{L}\Big) $$The solution from mathematica is:$$ \eta(x, t) = \sin\Big( 2 \cot^{-1} \Big[ e^{\frac{2 \pi t + L \log\Bigg[\cos\Big({\frac{\pi x}{L}\Big)}\Bigg] - L \log\Bigg[ \sin\Big({\frac{\pi x}{L}\Big)} \Bigg]}{L}} \Big] \Big) $$I solve the numerical version by integrating the PDE with respect to t, then, I get the follwing

$$ \eta(x, t + 1) = \eta(x, t) - \sin(2 \frac{\pi x}{L}) \frac{\Delta t }{\Delta x} [\eta(x+1, t) - \eta(x, t)] $$

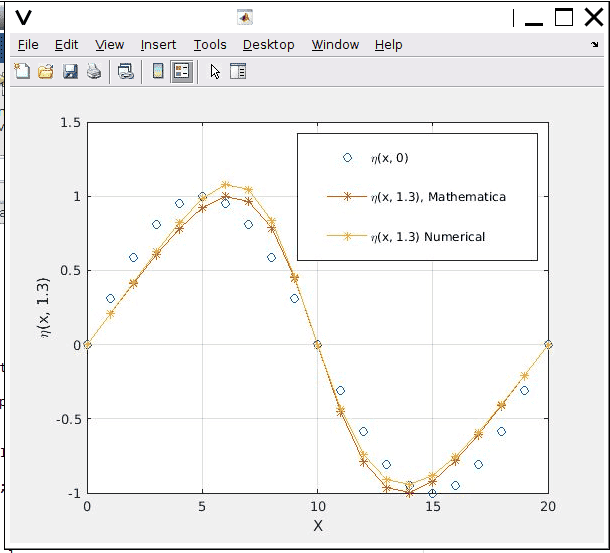
The results are given in the picture for x from 0 to 20 with a step of 1 and t from 0 to 1.3 with a step of 0.1.

However, they both satisfy the boundary conditions. The peak values are different.

 

[phyzguy]

The numerical solution will always have errors, since you are approximating a continuous function as a set of discrete data points. Try decreasing the size of the time step Δt, and possibly also the space grid spacing Δx. As you decrease those, the numerical solution should approach the Mathematica solution. Does it?

 

[tworitdash]

The numerical solution will always have errors, since you are approximating a continuous function as a set of discrete data points. Try decreasing the size of the time step Δt, and possibly also the space grid spacing Δx. As you decrease those, the numerical solution should approach the Mathematica solution. Does it?

Yes, indeed it does. As the paper had more accurate values at the peak with numerical solution (although they didn't show the solution), I was wondering. One interesting thing I tried yesterday. I changed the definition of the derivative with respect to space on the right hand side and applied Neuman's boundary condition at the edges (values of $\eta(x)$ don't change at the edges). Here, I use the terms in the brackets as indices. So, for example $\eta(x + 1, t) = \eta(x + \Delta x, t)$

$$ \frac{\partial\eta(x, t)}{\partial x} = \frac{\eta(x + 1) - \eta(x - 1)}{2 \Delta x} $$

Now the results have been improved.

 

[Fred Wright]

On examining your solution from mathematica I found a problem. For the initial condition,
$$
\eta (L,t) = 0
$$
the exponential argument of $\cot^{-1}$ is
$$
e^{\frac{\pi t}{L} + \log(-1)-\log(0)}=e^{\frac{\pi t}{L} + i\pi + \infty}
$$
That is, the argument is complex at the boundary condition. This bothers me, so I solved the problem using the method of characteristics. I get,
$$
\eta (x,t)=\sin(2\cot^{-1}(\frac{e^{ \left [ (\frac{-2\pi t}{L})+\log(2\sin(\sin(\frac{2\pi}{L}x))-\log (2\cos(\sin(\frac{2\pi}{L}x))))\right ]}}{2}))
$$
I don't have mathematica, but I suspect your numerical solution might be accurate but you may have made an error in however you input the problem to the mathematica software.

 

[pasmith]

On examining your solution from mathematica I found a problem. For the initial condition,
$$
\eta (L,t) = 0
$$
the exponential argument of $\cot^{-1}$ is
$$
e^{\frac{\pi t}{L} + \log(-1)-\log(0)}=e^{\frac{\pi t}{L} + i\pi + \infty}
$$

That is, the argument is complex at the boundary condition.

This bothers me, so I solved the problem using the method of characteristics. I get,
$$
\eta (x,t)=\sin(2\cot^{-1}(\frac{e^{ \left [ (\frac{-2\pi t}{L})+\log(2\sin(\sin(\frac{2\pi}{L}x))-\log (2\cos(\sin(\frac{2\pi}{L}x))))\right ]}}{2}))
$$
I don't have mathematica, but I suspect your numerical solution might be accurate but you may have made an error in however you input the problem to the mathematica software.

The Mathematica result is basically correct; it's just made the schoolboy error of using $\int 1/u\,du = \log u + C$ rather than $\int 1/u\,du = \log|u| + C$. However I don't think your result is correct.

The method of characteristics gives that $\eta$ is constant on curves $(x(t),t)$ where, for $x(0) \neq 0, L/2, L$,
$$\int_{x(0)}^{x(t)} \csc(2\pi x/L)\,dx = t$$ or $$\left[\ln|\csc(2\pi x/L) + \cot(2\pi x/L)|\right]_{x(0)}^{x(t)} = \left[\log |\cot(\pi x/L)|\right]_{x(0)}^{x(t)}= -2\pi t/L.$$ Solving this yields $$\cot(\pi x(t)/L) = \cot(\pi x(0)/L) e^{-2\pi t/L},$$ irrespective of the sign of$\cot(\pi x/L)$. Applying the initial condition then gives $$\eta(x,t) = \sin\left( 2 \operatorname{arccot}\left( \cot(\pi x/L) e^{2\pi t/L} \right) \right).$$ This holds also for $x(0) = 0, L/2, L$ where the characteristic is $(x,t) = (x(0),t)$ and the initial condition is $\eta(x_0,0) = 0$ provided one identifies $\operatorname{arccot}(\infty) = 0$. Simplifying the Mathematica expression will, for positive arguments of $\log$, reduce to the above.

 

[tworitdash]

The Mathematica result is basically correct; it's just made the schoolboy error of using $\int 1/u\,du = \log u + C$ rather than $\int 1/u\,du = \log|u| + C$. However I don't think your result is correct.

The method of characteristics gives that $\eta$ is constant on curves $(x(t),t)$ where, for $x(0) \neq 0, L/2, L$,
$$\int_{x(0)}^{x(t)} \csc(2\pi x/L)\,dx = t$$ or $$\left[\ln|\csc(2\pi x/L) + \cot(2\pi x/L)|\right]_{x(0)}^{x(t)} = \left[\log |\cot(\pi x/L)|\right]_{x(0)}^{x(t)}= -2\pi t/L.$$ Solving this yields $$\cot(\pi x(t)/L) = \cot(\pi x(0)/L) e^{-2\pi t/L},$$ irrespective of the sign of$\cot(\pi x/L)$. Applying the initial condition then gives $$\eta(x,t) = \sin\left( 2 \operatorname{arccot}\left( \cot(\pi x/L) e^{2\pi t/L} \right) \right).$$ This holds also for $x(0) = 0, L/2, L$ where the characteristic is $(x,t) = (x(0),t)$ and the initial condition is $\eta(x_0,0) = 0$ provided one identifies $\operatorname{arccot}(\infty) = 0$. Simplifying the Mathematica expression will, for positive arguments of $\log$, reduce to the above.

Nice Observation!