I cannot grasp simultaneity in Special Relativity

[Hypercube]

Hi everyone,

I'm struggling to grasp simultaneity in Special Relativity. Since I am struggling conceptually, I have posted my question here. But if you think this problem I made up modified should go to homework, I apologise (and feel free to move it).

Suppose we have two light sources, $L_1$ and $L_2$, with distance $d$ between them. We have an observer ($O_1$) located at the midpoint who can control (activate) these lights at any given time.

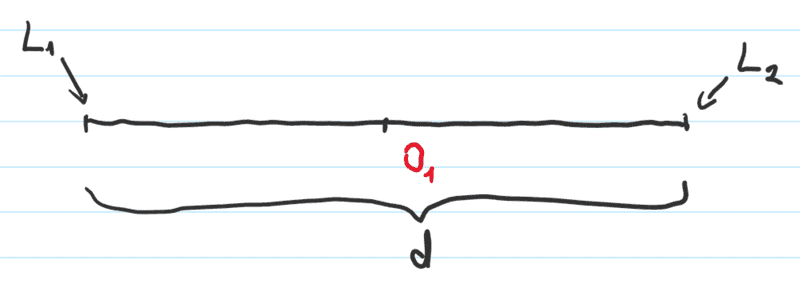
This observer measures proper distance between sources as $d$, and knows that every time he presses the switch, light rays meet at the midpoint. The time it takes for light to hit the midpoint is constant: $$\Delta t=\frac{d}{2c}$$

Next, suppose there is $O_2$ running towards $O_1$ in the positive $x$ direction. $O_1$ sees him moving with speed $V$ towards the centre.

In reference frame of $O_1$, as soon as $O_2$ gets to $V\Delta t$ from the centre, $O_1$ activates the light switches. Let's call this $t_0$. By the time $O_2$ gets to the centre, $O_1$ will observe light rays will "hit" the runner from both sides simultaneously. Let's call this $t_1$.

My question is - what does $O_2$ observe? How does the "world" look for him?

I know he will measure distance between the sources as $\frac{d}{\gamma}$, but does contraction occur symmetrical to his location? How does that affect simultaneity of events?

How do things "look" for him at $t=0$? Since he is closer to $L_1$ than to $L_2$, does that mean he sees $L_1$ first? But light was still transmitted simultaneously - just because you see light from one event sooner than light from another, that doesn't mean events happened at a different time, no?

 

[mfb]

O2 will measure that, at the time of the light emission, L1 was closer to him than L2 (the difference is $\frac{2v\Delta t}{\gamma}$) - but the light from both arrived at the same time. L1 must have switched on later.

 

[Hypercube]

(the difference is $\frac{2v\Delta t}{\gamma}$)

Ok, I'm following. I managed to derive this.

but the light from both arrived at the same time. L1 must have switched on later.

Ok, so the light sources switch on at different times, but light illuminates $O_2$ simultaneously. My intuition tells me that the faster $O_2$ moves, the greater is the the perceived discrepancy in activation of $L_1$ and $L_2$ (in his reference frame). Would you agree? And if so, is it possible to quantify the degree to which simultaneity brakes down (i.e. time interval between the two)?

All I know is how to compute time dilation of consecutive events using gamma. But I cannot use the gamma factor here, because these count as two events (plus, I'd be multiplying by 0, since $O_1$ sees them as simultaneous).

 

[Mister T]

$O_1$ will observe light rays will "hit" the runner from both sides simultaneously.

That's a single event, and as such it's invariant. All observers will agree on it.

My question is - what does $O_2$ observe?

The same thing, that the light rays hit simultaneously.

There is nothing relative about this kind of simultaneity. It's only when two separate events occur at two separate locations that simultaneity is relative.

The events in this case that demonstrate the relativity of simultaneity are the emissions of the light pulses. Those two events occur in two separate locations, and therefore they cannot be simultaneous for both $O_1$ and $O_2$.

In this case $O_1$ will conclude they're simultaneous, but $O_2$ will conclude that the flash coming from in front of him must have left first because it had to travel further.

 

[Mister T]

is it possible to quantify the degree to which simultaneity brakes down (i.e. time interval between the two)?

It doesn't break down, it's just that it's relative. The difference is $\frac{dv}{c^2}$.

 

[PeroK]

How do things "look" for him at $t=0$? Since he is closer to $L_1$ than to $L_2$, does that mean he sees $L_1$ first? But light was still transmitted simultaneously

You are, at least subconciously, looking at this problem as though $O_1$ and the lighting apparatus are "really" at rest and $O_2$ is really moving.

To see what happens in $O_2$'s reference frame you need a new diagram where $O_2$ is at rest and $O_1$ and the length-contracted lighting apparatus is moving towards him.

In this frame it's clear that the if the light emission events are simultaneous, then the light pulses do not reach $O_1$ simultaneously. And, if the light pulses reach $O_1$ simultaneously, then they cannot have been emitted simultaneously.

- just because you see light from one event sooner than light from another, that doesn't mean events happened at a different time, no?

That's true. It's far better to start thinking in terms of reference frames than raw observations. In any reference frame, in any physics, there is a time delay between a distant event and the light (or other) signal from that event reaching you. This has nothing to do with relativity.

If a clock chimes at 12 noon and you are a mile away, then you do not hear the chime until 5 seconds later. In your reference frame, you would need to take this into account. If another clock is nearer, say 1/5th of a mile, and also chimes at noon, then you will hear the chimes from that clock at 1 second past noon.

I'm assuming you and both clocks are all at rest relative to each other.

You will hear the two clocks chime at different times. But, assuming you know how far away the clocks are, you would calculate hence "observe" that the clocks both chimed at 12 noon.

In your reference frame, both clocks chimed at noon.

You need to do the same in relativitistic thought experiments by factoring out the travel time of light from any event.

 

[Hypercube]

@Mister T @PeroK
Thank you both for clarification.

I have a few more questions. This is perhaps a separate issue, but in terms of length contraction, what happens under limiting conditions as $V\rightarrow c$? Say, I am in a rocket and its engine exerts a constant force pushing me forward. Would I perceive forward direction "flattening"? All lengths in my direction of movement would continue to get shorter and shorter, yeah? So in the case of $v=c$ (I know, it cannot happen), would that imply that one spatial dimension in my reference frame would effectively disappear?

Also, suppose I am moving in that rocket with constant speed which is $v=0.999999995c$, and my goal is to reach some distant planet. My rocket can decelerate in infinitesimal fraction of time, somehow without turning my insides out. Based on what I calculated, I would have to start decelerating 2 metres from the surface of the planet, in order to appear 20 km in its orbit (since $\gamma = 10 000$). Does this make sense?

 

[Mister T]

This is perhaps a separate issue, but in terms of length contraction, what happens under limiting conditions as $V\rightarrow c$?

Just look at the function $\gamma=\frac{1}{\sqrt{1-(v/c)^2}}$. As $v \rightarrow c$, $\gamma \rightarrow \infty$. Thus lengths contract towards zero. Of course, $v$ can never equal $c$ so the length can never be zero. But there is otherwise no limit on how small it can be.

All lengths in my direction of movement would continue to get shorter and shorter, yeah?

Not all lengths, no. Only the lengths of things in motion relative to you, and then only along the direction of that motion.

So in the case of $v=c$ (I know, it cannot happen),

Then you are asking about something other than physics. What do the laws of physics have to say about things that violate the laws of physics?

Also, suppose I am moving in that rocket with constant speed which is $v=0.999999995c$, and my goal is to reach some distant planet. My rocket can decelerate in infinitesimal fraction of time, somehow without turning my insides out. Based on what I calculated, I would have to start decelerating 2 metres from the surface of the planet, in order to appear 20 km in its orbit (since $\gamma = 10 000$). Does this make sense?

Suppose a space buoy is somehow anchored relative to the planet, such that, in the rest frame of the planet, it's 20 km above its surface. You, headed directly for that planet, pass the space buoy and will measure the distance to the surface to be only 2 m. If that's what you mean, then, yes. In another 2 m, as measured in your rest frame, you will crash. But when measured in the rest frame of the planet, it's 20 km.

 

[Ibix]

e, but in terms of length contraction, what happens under limiting conditions as $V\rightarrow c$?
I am in a rocket and its engine exerts a constant force pushing me forward. Would I perceive forward direction "flattening"? All lengths in my direction of movement would continue to get shorter and shorter, yeah?

To you, you are always at rest. So nothing unusual happens. Relativistic effects are one of the few things that truly only happen to other people.

So in the case of $v=c$ (I know, it cannot happen), would that imply that one spatial dimension in my reference frame would effectively disappear?

You can't apply the Lorentz transforms (or special-case versions of them like the length contraction equation) to movement at c. The Lorentz transforms relate measurements in inertial frames in which the speed of light is always the same. "The rest frame of light" is a contradiction in terms because it would require light to be simultaneously stationary and moving at 3x10⁸m/s. Any conclusions you try to draw from a contradictory premise are nonsense.

Also, suppose I am moving in that rocket with constant speed which is $v=0.999999995c$, and my goal is to reach some distant planet. My rocket can decelerate in infinitesimal fraction of time, somehow without turning my insides out. Based on what I calculated, I would have to start decelerating 2 metres from the surface of the planet, in order to appear 20 km in its orbit (since $\gamma = 10 000$). Does this make sense?

Yes, particularly given the way @Mister T restated your problem. Adding a marker buoy as he did makes it absolutely clear where you intend to trigger the acceleration.

Relativity divides spacetime into three regions for any event - the past light cone, the future light cone, and the region outside either light cone. These concepts are the rigorous version of what we mean by "the past", "the future" and a third concept that we don't really have a layman's term for. In the case of your instantaneous deceleration, it makes sense for you to use your "planet is moving" frame coordinates in the past light cone of the deceleration, and to use your "planet is stationary" frame coordinates in the future light cone. But there's the third volume of spacetime which is outside your light cone and lies between the future and past light cones. It's possible to assign coordinates in that volume so that the planet moves smoothly from 2m to 20km. A surprisingly straightforward method is called radar coordinates - see Dolby and Gull (https://arxiv.org/abs/gr-qc/0104077).

 

[Hypercube]

Yes, buoy analogy was very helpful, it cleared up my misconception. Thank you both for your replies.