I with understanding Kepler's second law

[frostysh]

I have a lot of questions as usually, but must begin with the difficult to understand moment which have started my explorations of the Kepler's second law. In the book of Steven Wainberg "To Explain The World", in the technical paragraph twenty one I have found the next formula which represents somekind of a small area on plane$$\large \delta A = -\dfrac{1}{2} \times r_{+} \times 2\pi r_{+} \times \dfrac{\delta\theta}{360^{\circ}} = -\dfrac{1}{2R}r_{+}^{2} \delta\theta = -\dfrac{a^{2}}{2R}\left(\dfrac{1 - e^{2}}{1 - e\cos{\theta}}\right)^{2} \delta\theta,$$where $\delta A$ is an area which has cutting the segment from the Sun to the planet on it's elliptic orbit, $e$ — is an eccentricity of the orbit, $R$ is a coeficient, the result because the proportion is in degrees but not radians, and equal $R = 360^{\circ}/2\pi$. I think I will better just draw some picture, illustrations is very helpful indeed.

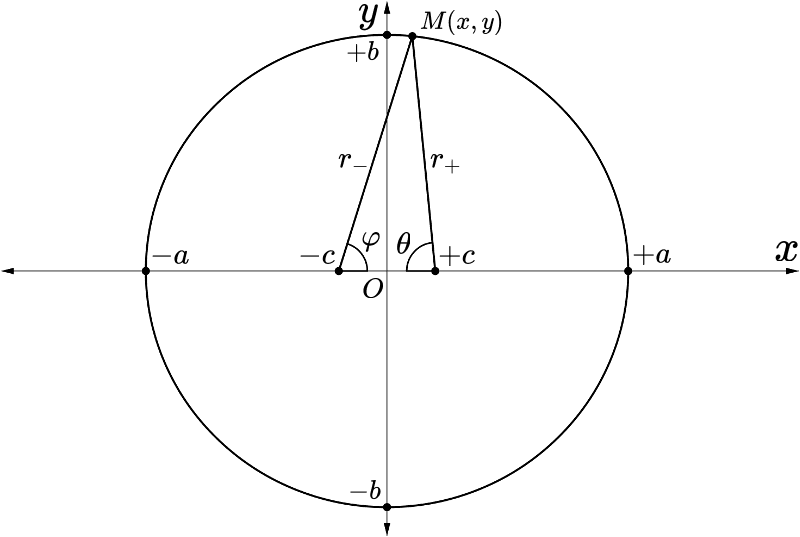
The Sun is in focus $+c$, the planet is in point $M$ with coordinates $\left(x, y\right)$.
My questions is: before the formula author of the book saying that it is an area $\delta A$ of the triangle which is equilateral, and it's base is on circle with radius $r_{+}$, but is this base are approximation of the ellipse, or the circle just intersect ellipse in the point $M$? Or this is no matters relative to the infinitely small values? I thanks for the future answers.

 

[jambaugh]

If one works with $\theta$ in radian measure you get:
$$\delta A = -\tfrac{1}{2} r_+^2 \delta \theta$$
This is a differential relation and assumes that $\delta A, \delta \theta,$ and $\delta r_+$ are all small. Note that if you simply vary $r_+$ (freely moving off the orbit) while leaving $\theta$ unchanged then you do not sweep out any area since you just get a longer line-segment in the same direction. The only contribution is when you vary the angle. Thus even if the object is not moving in a circle and has significant radial motion, the differential area will only be proportional to the differential angle.

So I think the answer to your question is that the equilateral triangle referred to is the one with base perpendicular to the radial line of length $r_+$. But it does not matter when the changes considered are very small.

For purposes of comparing the triangles with different "base" angles, you can treat the two long sides as if they were approximately parallel when the differential angle is approximately zero.

 

[frostysh]

If one works with θθ in radian measure you get:

δA=−12r2+δθδA=−12r+2δθ​

This is a differential relation and assumes that δA,δθ,δA,δθ, and δr+δr+ are all small. Note that if you simply vary r+r+ (freely moving off the orbit) while leaving θθ unchanged then you do not sweep out any area since you just get a longer line-segment in the same direction. The only contribution is when you vary the angle. Thus even if the object is not moving in a circle and has significant radial motion, the differential area will only be proportional to the differential angle.

Is the case is case of we approximating ellipse with a circle and saying that the result area is true for the all ellipses, this means we can avoid some mathematical analysis theorems (me poor knowledge in mathematical analysis)?

We can scribe that $MM' = \widehat{MM'}$, and the height $h = r_{+}$, so the equilateral triangle areas will be:$$S_{\triangle +cMM'} = \dfrac{1}{2}h \times MM' = \dfrac{1}{2}r_{+} \times \dfrac{2\pi r_{+} \delta\theta}{360^{\circ}} = \dfrac{1}{2R}r_{+}^{2} \delta\theta,$$ or it's another case, where we using sector areas?

And we can scribe result area as limit, and$$S_{\delta\theta} = \dfrac{\pi r_{+}^2 \delta\theta}{360^{\circ}}.$$Or it's cases in therm of words we saying different (first is less accurate), but in the final result is equal? Or they also equal due to the infinitely small values such as $\delta\theta$?

 

[sophiecentaur]

Or this is no matters relative to the infinitely small values? I thanks for the future answers.

I'm not going to come up with a specific answer here but it will all hang on the way that 'limits' work in Calculus. When you derive the methods of finding gradients of functions in Calculus, you work out the dimensions of a 'triangle' and then make it smaller and smaller until terms like δx² can be neglected compared with δx and leave yourself with a simple expression (the limit). If you are careful with your geometry you can apply it in all co-ordinate systems (e.g. polar). Personally, once I was shown the method at A Level, I just believe it works where I read it in a book. (!? sloppy or what)

PS The History of Science is interesting but the Maths in some old derivations may not be totally watertight. I wouldn't lose too much sleep about it because chasing up some of the oddities could involve a lot of in-depth research. Remember, Keppler's Laws were originally based on and 'confirmed' by a lot of measurements and not any fundamental 'Laws of Physics'.

 

[vanhees71]

Well, AFAIK Kepler was right with his mathematics.

I'm not sure, where the problem in the above derivation is. You only need two facts:

(1) Let a curve be given in spherical coordinates $(r,\theta)$ in the form $r=r(\theta)$ (as usual I measure $\theta$ in radians, i.e., a full circle is $r=\text{const}$ with $\theta \in [0,2 \pi]$). Then the radius vector swipes out an infinitesimal area $\mathrm{d} A$ when the angle $\theta$ changes by an infinitesimal amount of $\mathrm{d} \theta$, which is given by
$$\mathrm{d} A=\frac{\mathrm{d} \theta}{2 \pi} \pi r^2(\theta),$$
because for infinitesimal $\theta$ you can approximate the area by the area of the corresponding circular segment.

(2) An ellipse with the origin of the polar coordinates in one of its foci (exactly what you need for planetary motion, where you can consider the Sun sitting still at the origin of your coordinates) is given by
$$r(\theta)=\frac{p}{1-\epsilon \cos \theta},$$
where $\epsilon \in [0,1[$ is the excentricity, $\epsilon e/a$, and $p=b^2/a=a(1-\epsilon^2)$, where $2e$ is the distance between the foci, $a$ is the major and $b$ the minor half-axis. Obviously Weinberg acharacteristally counts the angle $\theta$ from the aphel rather than usual from the perihel, i.e., $\theta=0$ is the point of the largest distance of the planet from the Sun (aphel).

This means
$$r(\theta)=\frac{a(1-\epsilon)^2}{1-\epsilon \cos \theta},$$
and plugging this into the formula for the area you get Weinberg's formula (despite the fact that Weinberg measures the angle in degrees, which is why he has to put the conversion factor $R=180^{\circ}/\pi$ in the denominator).

 

[frostysh]

I'm not going to come up with a specific answer here but it will all hang on the way that 'limits' work in Calculus.

Of course the modern mathematical analysis (Calculus) is a very powerful tool in Physics, and even more, for an example what a meaning of area inside of the closed complicated line without it? But the question was about words what we are saying to obtain some formula in the particular case, when as I think (maybe wrong), we can not use some theorems of mathematical analysis.

Well, AFAIK Kepler was right with his mathematics.

I'm not sure, where the problem in the above derivation is. You only need two facts:

(1) Let a curve be given in spherical coordinates $(r,\theta)$ in the form $r=r(\theta)$ (as usual I measure $\theta$ in radians, i.e., a full circle is $r=\text{const}$ with $\theta \in [0,2 \pi]$). Then the radius vector swipes out an infinitesimal area $\mathrm{d} A$ when the angle $\theta$ changes by an infinitesimal amount of $\mathrm{d} \theta$, which is given by
$$\mathrm{d} A=\frac{\mathrm{d} \theta}{2 \pi} \pi r^2(\theta),$$
because for infinitesimal $\theta$ you can approximate the area by the area of the corresponding circular segment.

For now the polar coordinate system, the more preciously the formulas which represents the conical cuts such as ellipse there is too complicated for myself. But I will try to study the topic. Professor Wainberg know the true answer from the beginning, which can be obtained with accurate mathematics in polar coordinate systems too, of course.
Remarkable to say, that what I have discovered, it's the changing of from equidistant to non-equidistant motion when we little bit changing the form of the trajectory due to the formula of maximum and minimum speed difference$$v_{max} - v_{min} = \sqrt{GM}\sqrt{\dfrac{1}{a}}\left(\negthickspace\sqrt{\dfrac{1 + e}{1 - e}} - \sqrt{\dfrac{1 - e}{1 + e}}\right)\negthickspace,$$it's because of the maximum and minimum distance to the Sun and the energy conversation law as has been said to me on the other forum.

P. S. The image of formulas on this forum is no good, it's sometimes hard to distinguish epsilon from e.

 

[sophiecentaur]

Oh Kepler’s maths was good but did he know about the inverse square law, applied to Gravity? I thought that came later and that he was just looking at the measured geometry and timing measurements.

But the question was about words what we are saying to obtain some formula in the particular case, when as I think (maybe wrong), we can not use some theorems of mathematical analysis.

The point I'm making is that the step in his calculations that you are querying is explainable in terms of Calculus. It could be hard work to re-state each of his mathematical steps in a way that you find understandable. In another context, would you want to use Newton's version of calculus and his wording in order to 'believe' and understand his final results? Sounds like a very hard way through a problem which is soluble by modern methods and terminology. I know that History can be interesting but I just wonder when authenticity and 're-enactment' are worth the effort.

 

[vanhees71]

Kepler did not know about the inverse square law, nor was Newtonian mechanics even formulated. One should note that Kepler's work has been done in 1609, i.e., before the advent of Newtonian mechanics. Kepler used accurate data on the Mars orbit by Brahe to deduce his laws. This is a formidable task, given that he had no modern computers and that he had to transform to the heliocentric reference frame (as we'd call it today).

It was the other way around: Newton, after formulating his mechanical laws, thought about from which force law he could get Kepler's laws, and the answer was from the inverse-square-law central force, which was the discovery of the laws of gravitational interaction.

Today we use the Kepler problem as one of the most beautiful examples for the application of Newtonian mechanics. There's something to learn at all levels of sophistication. You can start from plain Newtonian mechanics, using the conservation laws for a closed system of two "particles" interacting via a central inverse-square force.

It comes out that Kepler's 2nd law holds true for any central-force interaction, because it's just the conservation of total angular momentum (in the center-of-mass frame of Sun and planet, but to a pretty good approximation also in the rest frame of the Sun, because for all planets in our solar system $m_{\text{planet}} \ll m_{\text{sun}}$). This also implies that the orbit is a planar curve.

The 1st Law can be derived from the equations of motion, using energy conservation, analytically leading to the orbit in the form $r=r(\theta)$, given above. It turns out that the possible orbits are all conical intersections, depending on the sign of the energy: $E<0$ are the bound orbits (ellipses), $E=0$ leads to a parabola, and $E>0$ to hyperbolas.

Kepler also managed to calculate the position of the planets as function of time, given the orbital parameters. To this end he transformed everything to the excentric angle, $u$, (counted from the center of the ellipse not from the focus) and could come up with an implicit formula, i.e., $t$ as a function of $u$. As a special application of the formula you also get Kepler's 3rd Law.

Of course the Kepler problem is also a playground for analytical mechanics (Hamilton's least-action principle and Noether's theorem). There it comes out that the Kepler problem has not only the usual spacetime symmetries that any closed Newtonian system must have but additional symmetries, leading to the conservation of the socalled Runge-Lenz vector, which points from the center of mass (or the Sun in the approximation mentioned above) to the perihel (or aphel) of the orbit, and that's the explanation, why you get a closed orbit (ellipse), i.e., no perihelion precession (which you get famously when treating the problem relativistically, where here you need general relativity, i.e., the motion of a planet as a "test particle" in the Schwarzschild spacetime with the Sun as "gravitational source").

 

[jambaugh]

Is the case is case of we approximating ellipse with a circle and saying that the result area is true for the all ellipses, this means we can avoid some mathematical analysis theorems (me poor knowledge in mathematical analysis)?

It is not a case of approximating an ellipse with a circle. It is more a case of 1.) equating a right trapezoid's area with the area of a rectangle formed by leveling the oblique side of the trapezoid by pivoting about the midpoint; and 2.) approximating a thin elliptical sector with the corresponding circular sector using the thinness to treat the two long sides as approximately parallel and the arcs as approximate line segments.

 

[vanhees71]

Usually one draws a circle around the center of the ellipse with the large semiaxis as radius to introduce the excentric angle, which is needed to solve for the time dependence of the orbit. For a very lucid derivation of the Kepler problem's solution using only elementary Newtonian mechanics, see

A. Sommerfeld, Lectures on Theoretical Physics, vol. 1

It's anyway recommended to read these lecture notes concerning all topics within classical physics. I think Sommerfeld's textbook series on theoretical physics (6 vols.) is still the best one ever written despite it's ~70 years old!