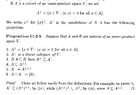Inner Product Spaces .... The Annihilator of a Set .... Garling, Proposition 11.3.5 - 1 ....

[Math Amateur]

I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume II: Metric and Topological Spaces, Functions of a Vector Variable" ... ...

I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...

I need some help to confirm my thinking on Proposition 11.3.5 - 1 ...

Garling's statement and proof of Proposition 11.3.5 reads as follows:
View attachment 8963
In Proposition 11.3.5 - 1, given the definition of \(\displaystyle A^{ \bot }\), we are required to prove that

\(\displaystyle A^{ \bot } = \{ x \in V \ : \ \langle a, x \rangle = 0\) for all \(\displaystyle a \in A \}\)

We need to show

\(\displaystyle A^{ \bot } = \{ x \in V \ : \ \langle x, a \rangle = 0\) for all \(\displaystyle a \in A \}\)
Proof:

By definition \(\displaystyle A^{ \bot } = \{ x \in V \ : \ \langle x, a \rangle = 0\) for all \(\displaystyle a \in A \}\)

\(\displaystyle \Longrightarrow A^{ \bot } = \{ x \in V \ : \ \overline{ \langle x, a \rangle } = 0\) for all \(\displaystyle a \in A \}\)
Now suppose \(\displaystyle \langle a, x \rangle = u + i v\)

Then \(\displaystyle \overline{ \langle x, a \rangle } = \langle a, x \rangle = u + i v\) by definition of an inner product ...

and so \(\displaystyle \langle x, a \rangle = u - i v\) Thus if \(\displaystyle \langle a, x \rangle = 0\) then \(\displaystyle u = v = 0\)

... which implies \(\displaystyle \langle x, a \rangle = 0\) Thus if

\(\displaystyle A^{ \bot } = \{ x \in V \ : \ \langle a, x \rangle = 0 for all a \in A \}\)

then

\(\displaystyle A^{ \bot } = \{ x \in V \ : \ \langle x, a \rangle = 0 for all a \in A \} \)

Is the above proof correct? Is there a better way to prove the above ...?Peter

 

[Olinguito]

Hi Peter.

You could just say
$$\langle a,x\rangle=0\ \iff\ \langle x,a\rangle=\overline{\langle a,x\rangle}=\overline 0=0.$$

 

[soloenergy]

Hi Peter,

Your proof looks correct to me. Another way to prove this proposition is by using the fact that the orthogonal complement is the set of all vectors that are perpendicular to the given set. So, we can show that A^{\bot} = \{x \in V : \langle x, a \rangle = 0 \text{ for all } a \in A\} by showing that every vector in A^{\bot} is perpendicular to every vector in A, and vice versa.

To show that every vector in A^{\bot} is perpendicular to every vector in A, we can use the definition of the inner product and the fact that the inner product is linear. Then, for any x \in A^{\bot} and a \in A, we have:

\langle x, a \rangle = \langle x, \sum_{i=1}^n \lambda_i a_i \rangle = \sum_{i=1}^n \lambda_i \langle x, a_i \rangle = \sum_{i=1}^n \lambda_i \cdot 0 = 0

where \lambda_i are scalars and a_i are vectors in A. This shows that x is perpendicular to every vector in A, and thus x \in A^{\bot}.

Similarly, to show that every vector in A^{\bot} is perpendicular to every vector in A, we can use the same argument in reverse. For any x \in A^{\bot} and a \in A, we have:

\langle a, x \rangle = \langle \sum_{i=1}^n \lambda_i a_i, x \rangle = \sum_{i=1}^n \lambda_i \langle a_i, x \rangle = \sum_{i=1}^n \lambda_i \cdot 0 = 0

This shows that a is perpendicular to every vector in A^{\bot}, and thus a \in A^{\bot}.

Therefore, we have shown that A^{\bot} = \{x \in V : \langle x, a \rangle = 0 \text{ for all } a \in A\}, and thus the proposition is proven.

I hope this helps! Let me know if you have any further questions or if you would like me to clarify anything. Happy studying!