- #1
mathmari
Gold Member
MHB
- 5,049
- 7
Hey! 
I want to draw the following spaces:
I want to draw the following spaces:
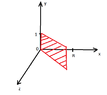
- $D_1=\{(x,y,z)\mid 0\leq x\leq 1, \ 1-x\leq y\leq 1, \ x\leq z\leq 1\}$
By the inequalities $0\leq x\leq 1, \ 1-x\leq y\leq 1$ we get a triangle on the $xy$-plane with vertices $(0,1)$, $(1,0)$ and $(1,1)$.
So, we have that triangle at the plane $z=0$. Do we shift that triangle to the plane $z=1$ because of the inequality $x\leq z\leq 1$, and so we get all the points between the triangle at $z=0$ till the triangle at $z=1$ ?
$$$$
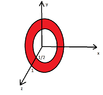
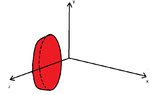
- $D_2=\left \{(x,y,z)\mid \frac{1}{2}\leq z\leq 1, \ x^2+y^2+z^2\leq 1\right \}$
$x^2+y^2+z^2\leq 1$ is a sphere. From the inequality $\frac{1}{2}\leq z\leq 1$ we take only one part of the sphere, or not?
$$$$
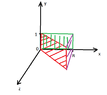
- $D_3=\{(x,y,z)\mid 0\leq x\leq \pi , \ 0\leq y \leq 1, \ 0\leq z\leq x\}$
We draw the line $z=x$ on the $xz$-plane for $0\leq x\leq \pi$. Since $0\leq y\leq 1$, we get the following parallelogramm:
View attachment 7396
Is this correct?
$$$$
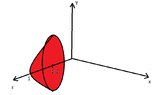
- $D_4$ is defined by the paraboloid with equation $z=2x^2+y^2$ and the cylinder with the equation $z=8-y^2$.
The paraboloid and the cylinder intersect at $2x^2+y^2=8-y^2 \Rightarrow x^2=4-y^2 \Rightarrow x=\pm \sqrt{4-y^2}$, therefore we get $-\sqrt{4-y^2}\leq x\leq \sqrt{4-y^2}$.
It must hold that $4-y^2\geq 0 \Rightarrow y^2\leq 4 \Rightarrow -2\leq y \leq 2$.
We have that $2x^2+y^2\leq 2\sqrt{4-y^2}^2+y^2=8-y^2 \Rightarrow 2x^2+y^2\leq z\leq 8-y^2$.
Therefore the space $D_4$ is the set $\{(x,y,z)\mid -\sqrt{4-y^2}\leq x\leq \sqrt{4-y^2}, \ -2\leq y \leq 2, \ 2x^2+y^2\leq z\leq 8-y^2\}$, or not?