- #1
Shawn Garsed
- 50
- 0
If the derivative of x^n equals nx^(n-1), then the derivative of x or x^1 equals x^0, but 0^0 is undefined. Does that mean x is not differentiable at zero?
Shawn Garsed said:If the derivative of x^n equals nx^(n-1), then the derivative of x or x^1 equals x^0, but 0^0 is undefined. Does that mean x is not differentiable at zero?
That's what it says in my book. That may not be the best answer, but that's where my question comes from.AdrianZ said:Why do you think 0^0 is undefined? 0^0 = 1.
No.Shawn Garsed said:If the derivative of x^n equals nx^(n-1), then the derivative of x or x^1 equals x^0, but 0^0 is undefined. Does that mean x is not differentiable at zero?
Shawn Garsed said:That's what it says in my book. That may not be the best answer, but that's where my question comes from.
HallsofIvy said:Please don't simply assert things (especially those others have already said were false) without giving some argument. What reason do you have to say that "0^0= 1"?
AdrianZ said:hmm, sounds strange to me. I'm not a math expert like others on this forum, but from what I know from abstract algebra, if we take ordinary multiplication as a binary operation, then for any x we have x^0 = 1 (the identity element), or generally in a group we have g^0=e for any g in G.
Do we really need to give any argument? Don't we define x^0 = 1 for any given x?
I like Serena said:R is not a group with multiplication, since 0 does not have an inverse.
You will need to specify a context for that definition, because contradictions are lurking around the corner.
EDIT: What should we do with 0^n for any given n?
AdrianZ said:That is exactly what I thought of. Please refresh. (I edited my previous post)
I can't say whether 0^0 is undefined or not, it seems that if we define 0^0=1 no contradiction would arise, but on the other hand as you rightly pointed out (and I had already thought of it) R is not a group under multiplication (R-{0} is), so my group theory argument is obviously wrong, but I'm not quite sure whether we could say 0^0=1 or not, because f(x)=x^x suggests us that it's possible to define 0^0=1.
D H said:The problem is by choosing different paths toward the origin, [itex]\lim_{x,y\to 0} x^y[/itex] can be made to have any value whatsoever. In other words, 0^0 is indeterminate (rather than undefined).
In many contexts such as the binomial expansion and the problem at hand, it is convenient to define 0^0 to be 1 as an abuse of notation. Extremely convenient, but still an abuse of notation.
I like Serena said:For f(x)=0^x you would define 0^0=0.
For f(x)=x^0 you would define 0^0=1.
In other words, you would define 0^0 depending on which function f you're talking about.
The only reason you would do something like that, is to get out from under the burden to meticulously define f(0) in each case.
AdrianZ said:Actually I was thinking of a similar kind of abuse of notation that DH said. It's not immediately clear why we should define 0! = 1, but it turns out to be very useful in infinite series and binomial expansions, it would be a very useful abuse of notation, but still an abuse of notation. lol.
Thanks.
D H said:0! = 1 is not an abuse of notation.
I like Serena said:Check out http://en.wikipedia.org/wiki/Empty_product.
As DH said, 0!=1 is well defined. ;)
History of differing points of view
Different authors interpret the situation above in different ways:
Some argue that the best value for 0^0 depends on context, and hence that defining it once and for all is problematic.[13] According to Benson (1999), "The choice whether to define 0^0 is based on convenience, not on correctness."[14]
Others argue that 0^0 is 1. According to p. 408 of Knuth (1992), it "has to be 1", although he goes on to say that "Cauchy had good reason to consider 0^0 as an undefined limiting form" and that "in this much stronger sense, the value of 0^0 is less defined than, say, the value of 0 + 0" (emphases in original).[15]
The debate has been going on at least since the early 19th century. At that time, most mathematicians agreed that 0^0 = 1, until in 1821 Cauchy[16] listed 0^0 along with expressions like 0⁄0 in a table of undefined forms. In the 1830s Libri[17][18] published an unconvincing argument for 0^0 = 1, and Möbius[19] sided with him, erroneously claiming thatwhenever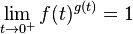 . A commentator who signed his name simply as "S" provided the counterexample of (e−1/t)t, and this quieted the debate for some time, with the apparent conclusion of this episode being that 00 should be undefined. More details can be found in Knuth (1992).[15]
. A commentator who signed his name simply as "S" provided the counterexample of (e−1/t)t, and this quieted the debate for some time, with the apparent conclusion of this episode being that 00 should be undefined. More details can be found in Knuth (1992).[15]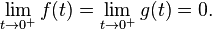
AdrianZ said:well, I read the page that ILS had given, I'm still not convinced why 0!=1 is well-defined (we define it this way!) but 0^0=1 is ill-defined.
Blame?AdrianZ said:It seems that we should blame Cauchy for this uninteresting discussion lol
Well, I'm convinced that defining 0^0 is ambiguous, but I'm not convinced why 0!=1 is well-defined yet. I read the page you said, I have no problem with it, it says that in general they define prod({})=1. It's a very reasonable definition, but my question is, is it the ONLY way that we can define it? I mean do we get contradictions if we define it in any other way? It's more like an 'uninteresting' question in logic rather than mathematics I think.I like Serena said:The difference is that 0^0 has different limits depending on the path you take to get there.
For 0! there is no such ambiguity: we're talking about integers only and only about multiplications of a whole number of factors.
Well, I dare to disagree with you on this. Euler didn't have a clear understanding of what he did with infinite series, but he's by far the most prolific mathematician in history and his results influenced many great mathematicians like Lagrange, Gauss, Cauchy, Riemann, Ramanujan and many others and his ideas are still influential in almost every area of mathematics, so he did his job properly and efficiently in my opinion and probably he never asked whether 0^0=1 or not. lol maybe I'm saying that because I think rigorists are ruining the beauty of mathematics and are making mathematics a sub area of logic forcefully but I personally prefer mathematical beauty to rigor and that's why I said we should blame Cauchy for this 'uninteresting' question. It's just a matter of taste and personal opinions I think xDBlame?
No, we should applaud his work, since he showed that the mathematicians before him hadn't done their job properly.
And now we have a consistent math framework (which leaves some things undefined LOL).
I like Serena said:@LikeMath: there is another special case for n=0.
However the formula also holds true for any ##n \in \mathbb{R}## if x>0.
X is not differentiable at x=0 because the function is not continuous at that point. This means that the limit of the function at x=0 does not exist, and therefore the function cannot have a well-defined derivative at that point.
You can tell if X is not differentiable at x=0 by checking if the function is continuous at that point. If the function is not continuous, then it is not differentiable at that point.
No, if X is not differentiable at x=0, it does not have a well-defined derivative at that point. However, it may still have a derivative at other points where it is continuous.
A function is continuous if it has no breaks or jumps in its graph. This means that the limit of the function as x approaches a certain value is equal to the value of the function at that point.
Not necessarily. X may not be differentiable at other points as well, depending on the nature of the function. It is important to check for continuity and differentiability at each point separately.