Level Curves and Partial Derivatives

[Lancelot1]

Hello everyone,

I am trying to solve this wee problem regarding partial derivatives, and not sure how to do so.

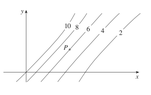
The following image shows level curves of some function \[z=f(x,y)\] :

View attachment 7998

I need to determine whether the following partial derivatives are positive or negative at the point P:

\[f_{x} , f_{y} , f_{xx} , f_{yy} , f_{xy} , f_{yx}\]

I am not sure how to relate the partial derivatives to the level curves. I know that partial derivatives at a point are slopes of a curve created when we fix a plane such as x=a or y=b. Where and how do I see it in level curves ?

Cheers !

 

[I like Serena]

Hi Lancelot,

Remember that a partial derivative is the limit of a slope.
More specifically:
$$
f_x(P)=\lim_{h\to 0}\frac{f(P+(h,0)) - f(P)}{h} \approx \frac{f(P+(h,0)) - f(P)}{h}
$$
Let's start at P and make a step with size $h>0$ to the right.
To the right of P we see that it has value 4.
And at P itself we have value 6.
So we have:
$$f_x(P)\approx \frac{4 - 6}{h} < 0$$
That is, the surface slopes down in the x-direction at point P.For the second partial derivative with respect to x we have:
$$f_{xx}(P) \approx \frac{f_x(P+(h,0)) - f_x(P)}{h}$$
We see that to the left the level curves are closer together than to the right.
That means that at left the slope is steeper than at the right.
So we take a small negative slope (at the right) minus a bigger negative slope (at the left), and end up with a positive number.
Or put otherwise, we begin with a steep downward slope, and have to add something positive to it to get a less steep slope.
So:
$$f_{xx}(P) > 0$$

How far do you get with the other partial derivatives?

 

[Lancelot1]

When I try to look at the derivate by y, I go up and down the y-axis, the level curves are constant there, am I wrong ?

 

[I like Serena]

When I try to look at the derivate by y, I go up and down the y-axis, the level curves are constant there, am I wrong ?

If we go up the y-axis starting from some arbitrary point, the level curve constants go up, don't they?
It means that $f_y > 0$.
That leaves the question how fast they go up.
Since the level curves are closer together for higher y, it means that the rate they go up accelerates.
Consequently $f_{yy} > 0$.