Lorentz group, boost and indices

[TimeRip496]

Compare this with the definition of the inverse transformation Λ^-1:

Λ^-1Λ = I or (Λ⁻¹)^α_νΛ^ν_β = δ_αβ,...(1.33)
where I is the 4×4 indentity matrix. The indexes of Λ⁻¹ are superscript for the first and subscript for the second as before, and the matrix product is formed as usual by summing over the second index of the first matrix and the first index of the second matrix. We see that the inverse matrix of Λ is obtained by

(Λ⁻¹)^α_ν = Λ_ν^α,.....(1.34)
which means that one simply has to change the sign of the components for which only one of the indices is zero (namely, Λ⁰_i and Λⁱ₀) and then transpose it:

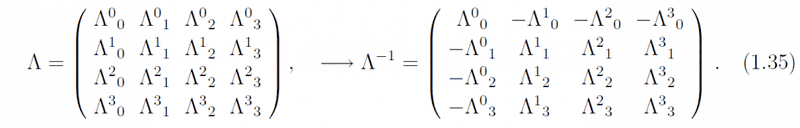
Source: http://epx.phys.tohoku.ac.jp/~yhitoshi/particleweb/ptest-1.pdf - Page 12

I understand everything except the bolded part. How does the author know to do that? Even if he meant to inverse the matrix in the conventional sense, it doesn't seems like it.

 

[TeethWhitener]

Try raising and lowering the indices $\nu$ and $\alpha$ on the Lorentz transformation with the metric tensor.

 

[TimeRip496]

Try raising and lowering the indices $\nu$ and $\alpha$ on the Lorentz transformation with the metric tensor.

You mean like
(Λ⁻¹)^α_ν = Λ_ν^α=Λ^ν_βg_vvg^βα

whereby $$g_{vv}=g^{βα}=
\begin{pmatrix}
1 & 0 & 0&0 \\
0 & -1 & 0&0 \\
0 & 0 & -1&0 \\
0 & 0 & 0&-1 \\
\end{pmatrix} $$

Just to confirm, the contraction between the two matrices can only be between alternate indices(as well as superscript and subscript) but not between the same indices of the matrices.

 

[TeethWhitener]

Try $\Lambda_{\nu}{}^{\alpha}=g^{\alpha\beta}g_{\mu\nu}\Lambda^{\mu}{}_{\beta}$

Just to confirm, the contraction between the two matrices can only be between alternate indices(as well as superscript and subscript) but not between the same indices of the matrices.

I'm not sure what this means. You can always sum over shared indices as long as one is up and the other is down.

 

[TimeRip496]

Try $\Lambda_{\nu}{}^{\alpha}=g^{\alpha\beta}g_{\mu\nu}\Lambda^{\mu}{}_{\beta}$

I'm not sure what this means. You can always sum over shared indices as long as one is up and the other is down.

$$g_{μv}=g^{αβ}=
\begin{pmatrix}
1 & 0 & 0&0 \\
0 & -1 & 0&0 \\
0 & 0 & -1&0 \\
0 & 0 & 0&-1 \\
\end{pmatrix} $$
$$g_{μv}.g^{αβ}=I$$
$$I.\Lambda^{\mu}{}_{\beta}=\Lambda^{\mu}{}_{\beta}$$
I know how the contraction in terms of Einstein notation works but I still can't get to its inverse in terms of the matrix. I try matrix product them but I still get back the original Lambda instead of its inverse. Did I get somewhere wrong here?

 

[TeethWhitener]

$g_{\mu\nu}g^{\alpha\beta}\neq I$. On the contrary, $g_{\mu\nu}g^{\nu\beta}=I$. That's the definition of matrix multiplication (which in this case is a contraction of a (2,2)-tensor over its inner indices to give a (1,1)-tensor).

Edit: it's probably easiest to just plug in a few numbers for the indices. For instance, try to evaluate $(\Lambda^{-1})^0{}_1$ using the equation for $\Lambda_{\nu}{}^{\alpha}$ that I mentioned in post #4.

 

[TimeRip496]

$g_{\mu\nu}g^{\alpha\beta}\neq I$. On the contrary, $g_{\mu\nu}g^{\nu\beta}=I$. That's the definition of matrix multiplication (which in this case is a contraction of a (2,2)-tensor over its inner indices to give a (1,1)-tensor).

Edit: it's probably easiest to just plug in a few numbers for the indices. For instance, try to evaluate $(\Lambda^{-1})^0{}_1$ using the equation for $\Lambda_{\nu}{}^{\alpha}$ that I mentioned in post #4.

I think I have something wrong with my understanding when it comes to operating them in terms of matrix.
$\Lambda_{\nu}{}^{\alpha}=g^{\alpha\beta}g_{\mu\nu}\Lambda^{\mu}{}_{\beta}= \begin{pmatrix} 1 & 0 & 0&0 \\ 0 & -1 & 0&0 \\ 0 & 0 & -1&0 \\ 0 & 0 & 0&-1 \\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0&0 \\ 0 & -1 & 0&0 \\ 0 & 0 & -1&0 \\ 0 & 0 & 0&-1 \\ \end{pmatrix} \begin{pmatrix} Λ^0{}_0 & Λ^0{}_1 & Λ^0{}_2&Λ^0{}_3 \\ Λ^1{}_0 & Λ^1{}_1 & Λ^1{}_2&Λ^1{}_3 \\ Λ^2{}_0 & Λ^2{}_1 & Λ^2{}_2&Λ^2{}_3 \\ Λ^3{}_0 & Λ^3{}_1 & Λ^3{}_2&Λ^3{}_3 \\ \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0&0 \\ 0 & -1 & 0&0 \\ 0 & 0 & -1&0 \\ 0 & 0 & 0&-1 \\ \end{pmatrix} \begin{pmatrix} Λ^0{}_0 & Λ^0{}_1 & Λ^0{}_2&Λ^0{}_3 \\ -Λ^1{}_0 & -Λ^1{}_1 & -Λ^1{}_2&-Λ^1{}_3 \\ -Λ^2{}_0 & -Λ^2{}_1 & -Λ^2{}_2&-Λ^2{}_3 \\ -Λ^3{}_0 & -Λ^3{}_1 & -Λ^3{}_2&-Λ^3{}_3 \\ \end{pmatrix}= \begin{pmatrix} Λ^0{}_0 & Λ^0{}_1 & Λ^0{}_2&Λ^0{}_3 \\ Λ^1{}_0 & Λ^1{}_1 & Λ^1{}_2&Λ^1{}_3 \\ Λ^2{}_0 & Λ^2{}_1 & Λ^2{}_2&Λ^2{}_3 \\ Λ^3{}_0 & Λ^3{}_1 & Λ^3{}_2&Λ^3{}_3 \\ \end{pmatrix}$
I did matrix product in between them as there are same indices and I don't know how to take the trace after tensor product. I think my problem is that I don't know how this works in terms of matrix.

 

[TeethWhitener]

It's probably better not to think of the problem in terms of matrices. Let's consider the specific example of $(\Lambda^{-1})^1{}_0 = \Lambda_0{}^1$. Lowering and raising indices gives us (with sums written explicitly)
$$\Lambda_0{}^1 = \sum_{\mu ,\beta} g^{1\beta}g_{\mu 0}\Lambda^{\mu}{}_{\beta}$$
But $g^{1\beta}$ will be zero unless $\beta=1$. Similarly, $g_{\mu 0}$ is only nonzero when $\mu =0$. This means the sum only has one nonzero term:
$$\Lambda_0{}^1 = g^{11}g_{00}\Lambda^{0}{}_{1}$$
Does this make it clear why 1) the indices flip, and 2) the sign changes when exactly one of the indices is zero?

 

[TimeRip496]

It's probably better not to think of the problem in terms of matrices. Let's consider the specific example of $(\Lambda^{-1})^1{}_0 = \Lambda_0{}^1$. Lowering and raising indices gives us (with sums written explicitly)
$$\Lambda_0{}^1 = \sum_{\mu ,\beta} g^{1\beta}g_{\mu 0}\Lambda^{\mu}{}_{\beta}$$
But $g^{1\beta}$ will be zero unless $\beta=1$. Similarly, $g_{\mu 0}$ is only nonzero when $\mu =0$. This means the sum only has one nonzero term:
$$\Lambda_0{}^1 = g^{11}g_{00}\Lambda^{0}{}_{1}$$
Does this make it clear why 1) the indices flip, and 2) the sign changes when exactly one of the indices is zero?

I think I get it and I know why my above matrix doesn't work cause my metric did not affect the indices of the original Λ matrix. Does it work if I see it in matrix like this?
$\Lambda_{\nu}{}^{\alpha}=g^{\alpha\beta}g_{\mu\nu}\Lambda^{\mu}{}_{\beta}= \begin{pmatrix} g^{00} & g^{01} & g^{02}&g^{03} \\ g^{10} & g^{11} & g^{12}&g^{13} \\ g^{20} & g^{21} & g^{22}&g^{23} \\ g^{30} & g^{31} & g^{32}&g^{33} \\ \end{pmatrix} \begin{pmatrix} g_{00} & g_{01} & g_{02}&g_{03} \\ g_{10} & g_{11} & g_{12}&g_{13} \\ g_{20} & g_{21} & g_{22}&g_{23} \\ g_{30} & g_{31} & g_{32}&g_{33} \\ \end{pmatrix} \begin{pmatrix} Λ^0{}_0 & Λ^0{}_1 & Λ^0{}_2&Λ^0{}_3 \\ Λ^1{}_0 & Λ^1{}_1 & Λ^1{}_2&Λ^1{}_3 \\ Λ^2{}_0 & Λ^2{}_1 & Λ^2{}_2&Λ^2{}_3 \\ Λ^3{}_0 & Λ^3{}_1 & Λ^3{}_2&Λ^3{}_3 \\ \end{pmatrix}$

 

[TeethWhitener]

If you do want to think in terms of matrices, make sure you're actually doing matrix multiplication: $\mathbf{AB} = A_{ij}B^{jk}$. The indices have to be matched up in a way that the summed-over index (j in this case) is on the inside of the products. So $g^{\alpha\beta}g_{\mu\nu}\Lambda^{\mu}{}_{\beta}$ isn't a valid form to represent matrix multiplication. There is a way to arrange this equation (and ONLY this equation) using the properties of the metric tensor so that you can matrix multiply: $g^{\alpha\beta}g_{\mu\nu}\Lambda^{\mu}{}_{\beta} = g_{\nu\mu}\Lambda^{\mu}{}_{\beta}g^{\beta\alpha}$. This second equation represents a matrix multiplication. You can do this because of the fact that the metric tensor is symmetric.

 

[TimeRip496]

If you do want to think in terms of matrices, make sure you're actually doing matrix multiplication: $\mathbf{AB} = A_{ij}B^{jk}$. The indices have to be matched up in a way that the summed-over index (j in this case) is on the inside of the products. So $g^{\alpha\beta}g_{\mu\nu}\Lambda^{\mu}{}_{\beta}$ isn't a valid form to represent matrix multiplication. There is a way to arrange this equation (and ONLY this equation) using the properties of the metric tensor so that you can matrix multiply: $g^{\alpha\beta}g_{\mu\nu}\Lambda^{\mu}{}_{\beta} = g_{\nu\mu}\Lambda^{\mu}{}_{\beta}g^{\beta\alpha}$. This second equation represents a matrix multiplication. You can do this because of the fact that the metric tensor is symmetric.

Thanks a lot!

 

[TeethWhitener]

No problem. A lot of the time, for me at least, explicitly writing out the sums helps me figure out what's going on (even if it's a bit tedious).