Mechanics- connected particles

[Shah 72]

Two smooth pulleys are 8m apart at the same horizontal level. A light inextensible rope passes over the pulleys and a box of mass 5kg hangs at each end of the rope. A third box of mass m kg is attached to the midpoint of the rope and hangs between the pulleys so that all the three boxes are at the same horizontal

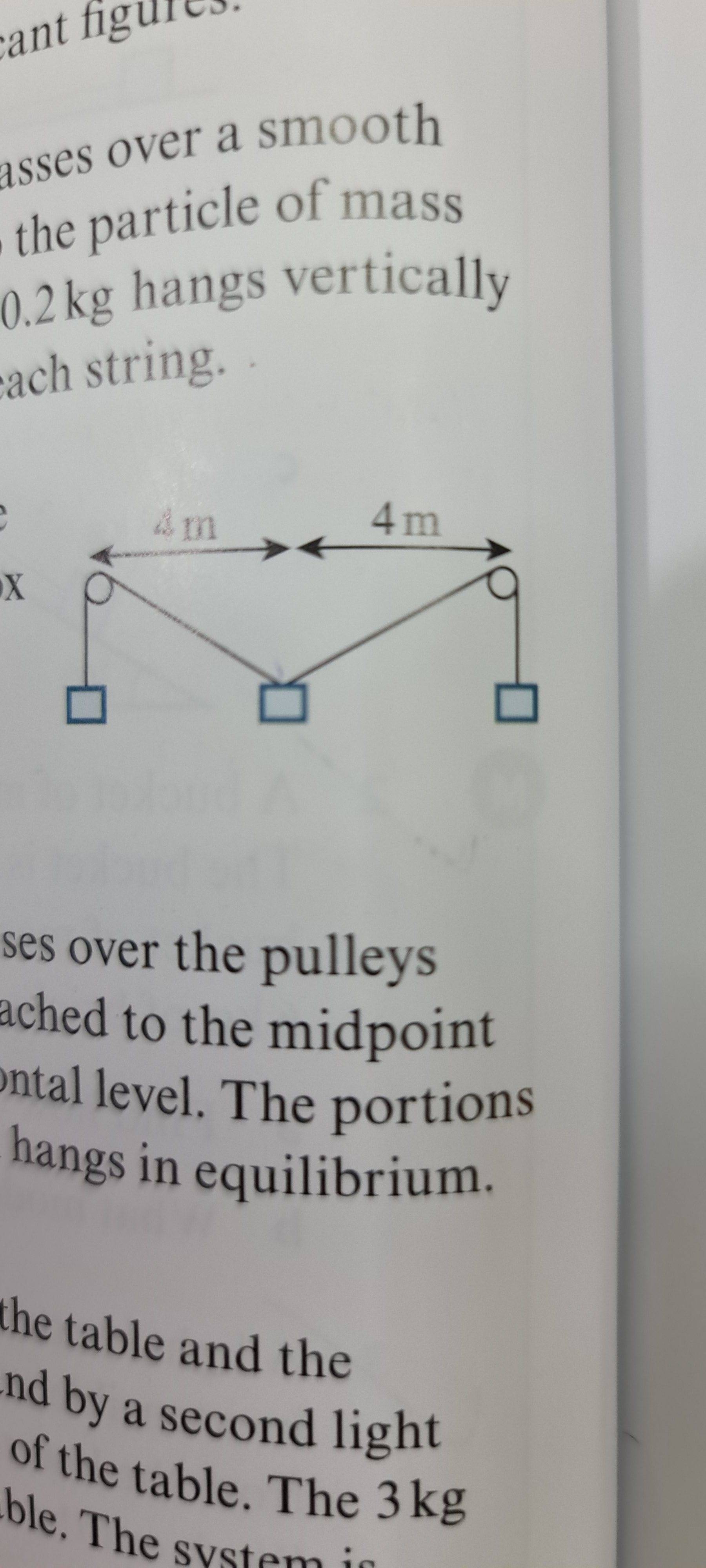level. The total length of the box is 16m. Find the value of m

 

[skeeter]

total length of the box? … maybe the string length is 16 m ?

if so, I get m = 7.5 kg

 

[Shah 72]

total length of the box? … maybe the string length is 16 m ?

if so, I get m = 7.5 kg

Iam so so sorry again typo error. Its the total length of the rope = 16m

 

[Shah 72]

total length of the box? … maybe the string length is 16 m ?

if so, I get m = 7.5 kg

The ans in the textbook says 6 kg.

 

[Shah 72]

total length of the box? … maybe the string length is 16 m ?

if so, I get m = 7.5 kg

Can you pls pls tell me how to work it out?

 

[skeeter]

The ans in the textbook says 6 kg.

6 kg is correct … I used the wrong value for a trig ratio.

 

[Shah 72]

6 kg is correct … I used the wrong value for a trig ratio.

Can you pls pls tell me the method you worked it out? I have no clue how to solve it.

 

[skeeter]

 

[Shah 72]

View attachment 11164

I have no clue how to do it. Sin theta= h/ sq root(h^2+16).

 

[skeeter]

$h + \sqrt{h^2+16} = 8$

…

 

[Shah 72]

$h + \sqrt{h^2+16} = 8$

…

By squaring both sides I will get 2h^2=-8 .

 

[skeeter]

$h + \sqrt{h^2+16} = 8$

$\sqrt{h^2+16} = 8-h$

square both sides …

$h^2+16 = 64 - 16h + h^2$

$16h = 48$

$h =3$

check solution …

$3 + \sqrt{3^2+16} = 3 + 5 = 8$

checks good.

recommend you review solving radical equations …

 

[Shah 72]

$h + \sqrt{h^2+16} = 8$

$\sqrt{h^2+16} = 8-h$

square both sides …

$h^2+16 = 64 - 16h + h^2$

$16h = 48$

$h =3$

check solution …

$3 + \sqrt{3^2+16} = 3 + 5 = 8$

checks good.

recommend you review solving radical equations …

Thank you so so much! None of these things are explained in the textbook. Iam really struggling with the pulley and string questions. I will surely look into solving radical equations.