- #1
- 22,183
- 3,321
In this thread, I present a few challenging problems from all kinds of mathematical disciplines.
RULES:
1. SOLVED BY andrewkirk Let's work in the unit square ##[0,1]\times [0,1]##. I pick two numbers at random from this unit square (with uniform distribution). What is the average length between these two numbers? What is the median length? What is the modus?
2. SOLVED BY QuantumQuest Find the sum of the reciprocals of a) the triangular numbers b) the square numbers c) the pentagonal numbers.
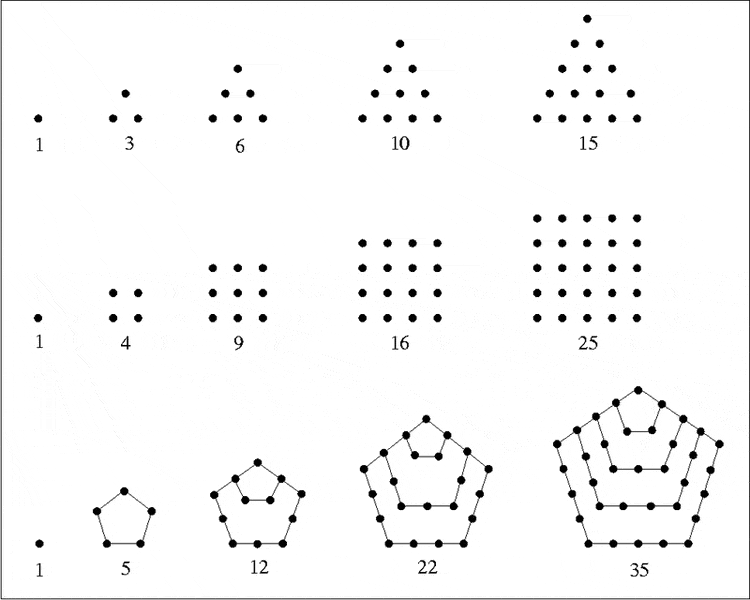
3. SOLVED BY mfb A man who owns ##r## umbrellas wanders back and forth between home and office, taking along an umbrella (if there is one at hand) in rain (it rains with probability ##p##), but not in sunshine (which happens with probability ##1-p##). Interpret and show the following statement: five umbrellas will protect the man at the ##5\%## level against again climate (i.e.\ any ##p##).
4. SOLVED BY Erland Consider on ##\mathbb{R}## the smallest class ##\mathcal{B}## of functions ##f:\mathbb{R}\rightarrow \mathbb{R}## containing all continuous functions and closed under pointswise limits. Show that ##\mathcal{B}## consists exactly of the Borel measurable functions.
5. SOLVED BY fresh_42 Find all groups of order ##p^2## where ##p## is a prime number. Do the same for groups of order ##p^3##.
6. SOLVED BY mfb, PeroK What is the probability that in a village with ##2016## inhabitants, every day is a birthday. Ignore leap years. Approximate solutions are acceptable, if you show that the approximation holds true in the limit.
7. SOLVED BY fresh_42 The set of ##2\times 2## matrices with integer entries and determinant ##1## is denoted by ##SL_2(\mathbb{Z})##. Show that this group is generated by the matrices
[tex]s = \left(\begin{array}{cc} 0 & -1\\ 1 & 0\end{array}\right)~\text{and}~s = \left(\begin{array}{cc} 1 & 1\\ 0 & 1\end{array}\right)[/tex]
Show furthermore that the group cannot be generated by a single element.
8. SOLVED BY fresh_42 Show that ##SO_3(\mathbb{R})## contains free groups of arbitrary finite orders.
9. SOLVED BY fresh_42 Let ##H## and ##K## be (not necessarily normal!) subgroups of a group ##G##. Show that
[tex]|HK|\cdot |H\cap K| = |H|\cdot |K|[/tex]
where ##HK = \{hk~\vert~h\in H,~k\in K\}##.
10. SOLVED BY Infrared Let ##(X,d)## be a metric space. Show that ##X## is compact if and only if for every continuous function ##f:X\rightarrow \mathbb{R}## holds that ##f(X)## is bounded.
RULES:
- In order for a solution to count, a full derivation or proof must be given. Answers with no proof will be ignored.
- It is fine to use nontrivial results without proof as long as you cite them and as long as it is "common knowledge to all mathematicians". Whether the latter is satisfied will be decided on a case-by-case basis.
- If you have seen the problem before and remember the solution, you cannot participate in the solution to that problem.
- You are allowed to use google, wolframalpha or any other resource. However, you are not allowed to search the question directly. So if the question was to solve an integral, you are allowed to obtain numerical answers from software, you are allowed to search for useful integration techniques, but you cannot type in the integral in wolframalpha to see its solution.
- Some of the solutions of (parts of) the following questions are not known to the author of this thread. So it might be that the question is unsolvable. No, I will not tell you which questions.
1. SOLVED BY andrewkirk Let's work in the unit square ##[0,1]\times [0,1]##. I pick two numbers at random from this unit square (with uniform distribution). What is the average length between these two numbers? What is the median length? What is the modus?
2. SOLVED BY QuantumQuest Find the sum of the reciprocals of a) the triangular numbers b) the square numbers c) the pentagonal numbers.
3. SOLVED BY mfb A man who owns ##r## umbrellas wanders back and forth between home and office, taking along an umbrella (if there is one at hand) in rain (it rains with probability ##p##), but not in sunshine (which happens with probability ##1-p##). Interpret and show the following statement: five umbrellas will protect the man at the ##5\%## level against again climate (i.e.\ any ##p##).
4. SOLVED BY Erland Consider on ##\mathbb{R}## the smallest class ##\mathcal{B}## of functions ##f:\mathbb{R}\rightarrow \mathbb{R}## containing all continuous functions and closed under pointswise limits. Show that ##\mathcal{B}## consists exactly of the Borel measurable functions.
5. SOLVED BY fresh_42 Find all groups of order ##p^2## where ##p## is a prime number. Do the same for groups of order ##p^3##.
6. SOLVED BY mfb, PeroK What is the probability that in a village with ##2016## inhabitants, every day is a birthday. Ignore leap years. Approximate solutions are acceptable, if you show that the approximation holds true in the limit.
7. SOLVED BY fresh_42 The set of ##2\times 2## matrices with integer entries and determinant ##1## is denoted by ##SL_2(\mathbb{Z})##. Show that this group is generated by the matrices
[tex]s = \left(\begin{array}{cc} 0 & -1\\ 1 & 0\end{array}\right)~\text{and}~s = \left(\begin{array}{cc} 1 & 1\\ 0 & 1\end{array}\right)[/tex]
Show furthermore that the group cannot be generated by a single element.
8. SOLVED BY fresh_42 Show that ##SO_3(\mathbb{R})## contains free groups of arbitrary finite orders.
9. SOLVED BY fresh_42 Let ##H## and ##K## be (not necessarily normal!) subgroups of a group ##G##. Show that
[tex]|HK|\cdot |H\cap K| = |H|\cdot |K|[/tex]
where ##HK = \{hk~\vert~h\in H,~k\in K\}##.
10. SOLVED BY Infrared Let ##(X,d)## be a metric space. Show that ##X## is compact if and only if for every continuous function ##f:X\rightarrow \mathbb{R}## holds that ##f(X)## is bounded.
Last edited: