aggie1293
- 2
- 0
I have a question pertaining to the motion of the center of mass (CM) of several connected bodies.
Here is a picture of the set-up (green surfaces are stationary):
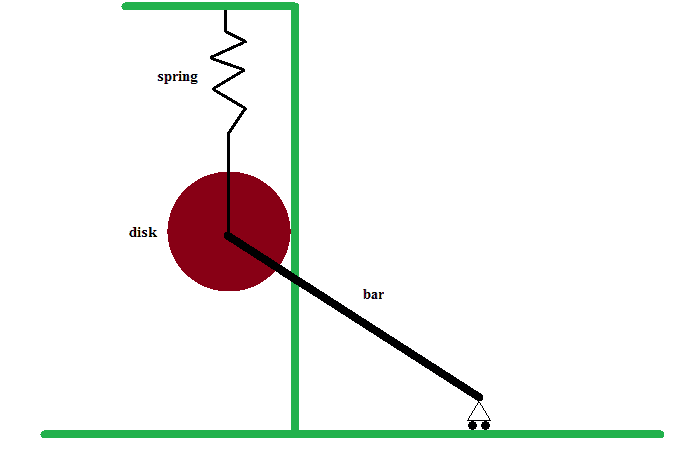 The mass of the spring is zero.
The mass of the spring is zero.
The mass of the disk is M1.
The mass of the bar is M2.
There is a pin reaction at the union of the bar and the disk, so the disk is free to rotate.
QUESTION: Will the disk touch the stationary wall at t>0?
F=Ma
First of all, assume that the disk will remain in contact with the wall as it falls. This would force the center of mass of the bar to move to the right, as in the picture below.
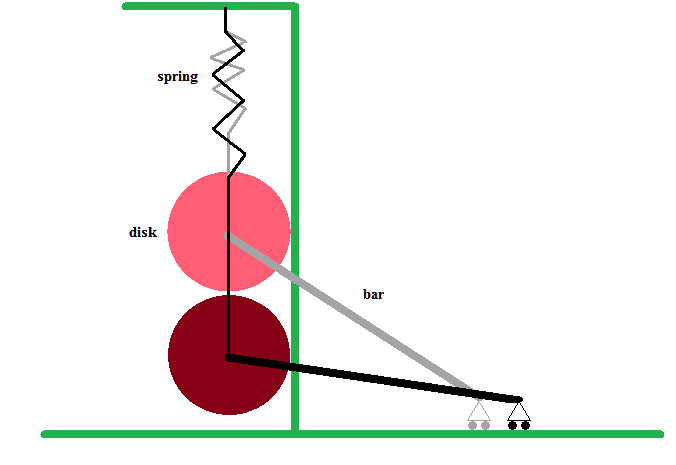
Since the CM of the disk does not horizontally and the CM of the bar moves to the right, the CM of the entire system also moves to the right. This is impossible because there is no force pushing any part of the system to the right.
 .
.
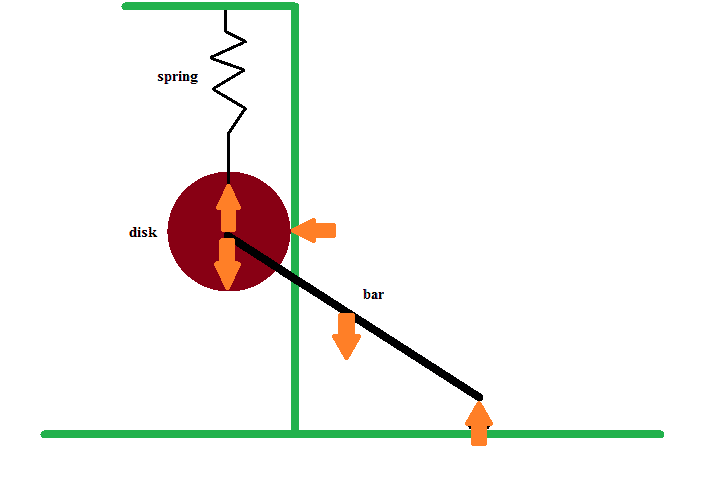
The orange arrows are the external forces acting on the body. Since there are no arrows pointing to the right (and the normal force can't be negative), there is no way for the CM of the system to move to the right.
Therefore, the assumption that the disk will remain on the wall is wrong. The disk will swing out as the reaction force of the bar resisting a change in it's inertia pushes it to the left. The reason I am asking this is because my professor and TA are adamant that the disk will roll down the surface of the wall. They say that Newton's second law is only applicable to rigid bodies.
Am I missing something here?
Homework Statement
Here is a picture of the set-up (green surfaces are stationary):
The mass of the disk is M1.
The mass of the bar is M2.
There is a pin reaction at the union of the bar and the disk, so the disk is free to rotate.
QUESTION: Will the disk touch the stationary wall at t>0?
Homework Equations
F=Ma
The Attempt at a Solution
I believe no, the reason being thus:First of all, assume that the disk will remain in contact with the wall as it falls. This would force the center of mass of the bar to move to the right, as in the picture below.
Since the CM of the disk does not horizontally and the CM of the bar moves to the right, the CM of the entire system also moves to the right. This is impossible because there is no force pushing any part of the system to the right.
The orange arrows are the external forces acting on the body. Since there are no arrows pointing to the right (and the normal force can't be negative), there is no way for the CM of the system to move to the right.
Therefore, the assumption that the disk will remain on the wall is wrong. The disk will swing out as the reaction force of the bar resisting a change in it's inertia pushes it to the left. The reason I am asking this is because my professor and TA are adamant that the disk will roll down the surface of the wall. They say that Newton's second law is only applicable to rigid bodies.
Am I missing something here?
Last edited: