Optics reflection/refraction problem

[raindrops]

Homework Statement

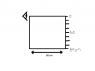
The 80 cm tall, 65 cm wide tank shown in the figure is completely filled with water (n=1.33). The tank has marks every 10 cm along one wall, and the 0 cm mark is barely submerged. As you stand beside the opposite wall, your eye is level with the top of the water.

a.) Can you see the marks from the top of the tank (the 0cm mark) going down, or from the bottom of the tank (the 80cm mark) coming up? Explain

b.) Which is the lowest or highest mark, depending on the your answer to part a, that you can see?

Homework Equations

I'm not sure what equations are relevant. maybe snell's law? n1sin$$\vartheta$$2=n2sin$$\vartheta$$2

The Attempt at a Solution

I'm really not sure where to even start.
** drawing is attached.

 

[zachzach]

Sketch the rays coming form the marks to your eye.

 

[raindrops]

He's looking for a mathematical answer, not just a drawing. Any ideas on how to do that?