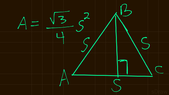Prove Area of Equilateral Triangle

[mathdad]

In chapter 6, section 6.1 of David Cohen's Precalculus textbook Third Edition, page 368, I found an interesting geometry problem.

Show that the area of an equilateral triangle of side s is given as shown in the picture.

The hint given is this:

Draw an altitude and use the Pythagorean theorem.

I drew an equilateral triangle and labelled each side s. I then drew an altitude from B to AC.

I don't know, however, where the sqrt{3} and 4 come from as shown in the picture. This is where I'm stuck. Can someone take me to the next step without completing the prove?

View attachment 7898

 

[MarkFL]

In the right triangle you've labeled with the right angle, what is the length of the shorter leg?

 

[mathdad]

In the right triangle you've labeled with the right angle, what is the length of the shorter leg?

You are talking about a 30°- 60° - 90° triangle with a short distance opposite 30 degrees, and it just so happens to be 1.

 

[HOI]

No, not the way you've shown this. You have an equilateral triangle with each side of length "S". The altitude of an equilateral triangle is (1) perpendicular to the opposite side, (2) bisects the angle, and (3) bisects the opposite side. So if each side of the equilateral triangle has length "S" and the altitude bisects a side, what is the length of the short side of the triangle? Then use the Pythagorean theorem to determine the length of the altitude.

 

[mathdad]

The length of the shortest side is s/2.

- - - Updated - - -

Let A = altitude

A^2 + (s/2)^2 = s^2

Is this the correct set up?

 

[mathdad]

When I solve A^2 + (s/2)^2 = s^2 for A, I get [s•sqrt{3}]/2. This is not right.

 

[Greg]

$$\triangle{ABC}=\frac{s}{2}\cdot s\sin60^\circ=\frac{s}{2}\cdot\frac{s\sqrt3}{2}=\frac{\sqrt3s^2}{4}$$

Using the Pythagorean theorem and $\triangle{ABC}=\frac{b\cdot h}{2}$, where $b$ is the length of the base of the triangle and $h$ is the height,

$$\triangle{ABC}=\sqrt{s^2-\frac{s^2}{4}}\cdot\frac s2=\sqrt{\frac{3s^2}{4}}\cdot\frac s2=\frac{\sqrt3s}{2}\cdot\frac s2=\frac{\sqrt3s^2}{4}$$

 

[mathdad]

$$\triangle{ABC}=\frac{s}{2}\cdot s\sin60^\circ=\frac{s}{2}\cdot\frac{s\sqrt3}{2}=\frac{\sqrt3s^2}{4}$$

Using the Pythagorean theorem and $\triangle{ABC}=\frac{b\cdot h}{2}$, where $b$ is the length of the base of the triangle and $h$ is the height,

$$\triangle{ABC}=\sqrt{s^2-\frac{s^2}{4}}\cdot\frac s2=\sqrt{\frac{3s^2}{4}}\cdot\frac s2=\frac{\sqrt3s}{2}\cdot\frac s2=\frac{\sqrt3s^2}{4}$$

You guys are truly amazing mathematicians. I thought the shortest side is s/2. I was wrong. Solving A^2 + (s/2)^2 = s^2 for A is wrong. I wonder what I did wrong in my computation.

 

[HOI]

When you divide the equilateral triangle into two right triangles to use the Pythagorean theorem to get the height, the base of each right triangle is s/2. But the base of the original equilateral triangle is twice that- s.

 

[mathdad]

When you divide the equilateral triangle into two right triangles to use the Pythagorean theorem to get the height, the base of each right triangle is s/2. But the base of the original equilateral triangle is twice that- s.

Yes, I forgot. The base of the original triangle is (s/2) + (s/2) = s.