Prove centre of mass of an arc is rotationally invariant

[Happiness]

Suppose the coordinates $(\bar{x}, \bar{y})$ of the centroid (or the centre of mass) of an arc is defined as follows

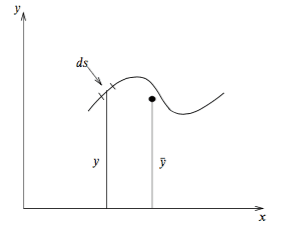
$\bar{x}=\frac{1}{L}\int x\,ds$ and $\bar{y}=\frac{1}{L}\int y\,ds$, where $L$ is the arc length.

Could you prove that the centroid is invariant under a rotation of the coordinate axes?

 

[chiro]

Hey Happiness.

Have you tried doing a substitution that allows you to rotate everything?

Hint - Try using polar co-ordinates.

 

[Happiness]

Hey Happiness.

Have you tried doing a substitution that allows you to rotate everything?

Hint - Try using polar co-ordinates.

Hey chiro

Yes I've considered doing that for a specific example, $y=x^3-4x^2+x+12$, but it is very tedious and the integration we get is most likely not do-able. And even if we can perform the integration, we would only prove it for a specific case.

I'm thinking using matrices may help, but I'm not sure how.

 

[chiro]

If you want to use matrices then just expand the linear combination in terms of x as a function of r and theta.

What you will find is that it's exactly the same as the integral.

When you did the substitution - did you go to (r,theta) space and if so what did you get when doing so?

Note that for 2D polar you have x = rcos(theta), y = rsin(theta) and the Jacobian is r.

What you will have to show is that your integral as a function of theta is the same so this means your integral won't be a function of theta at all (i.e. it disappears).

If you show this in general you have proved the invariance property.

 

[Happiness]

Is this correct?

Under polar coordinates, the definitions of $\bar{x}$ and $\bar{y}$ become

$\bar{r}\cos\bar{\theta}=\frac{1}{L}\int_{\theta_1}^{\theta_2}r(\theta)\cos\theta\sqrt{r^2(\theta)+(\frac{dr(\theta)}{d\theta})^2}d\theta$

$\bar{r}\sin\bar{\theta}=\frac{1}{L}\int_{\theta_1}^{\theta_2}r(\theta)\sin\theta\sqrt{r^2(\theta)+(\frac{dr(\theta)}{d\theta})^2}d\theta$

where $\bar{r}$ is the magnitude of the position vector $\vec{r}$ of the centroid and $\bar{\theta}$ is the angle the position vector $\vec{r}$ makes with the positive x-axis. ($\bar{r}$ and $\bar{\theta}$ may not necessarily be the average values of $r$ and $\theta$. Would they necessarily and sufficiently be so?) $r^2(\theta)$ means $r^2$ is a function of $\theta$.

Consider a rotation of the coordinate axes by an angle $\alpha$ clockwise. Then the point $(r, \theta)\to(r, \theta+\alpha)$ and the value $r(\theta)\to r(\theta+\alpha)$. [$r(\theta+\alpha)$ means for every $\theta$ in $r(\theta)$ we substitute $\theta+\alpha$.] We have

$\bar{x}'=\frac{1}{L}\int_{\theta_1+\alpha}^{\theta_2+\alpha}r(\theta+\alpha)\cos(\theta+\alpha)\sqrt{r^2(\theta+\alpha)+(\frac{dr(\theta+\alpha)}{d\theta})^2}d\theta$

where the $\bar{x}'$ is the x-coordinate of the centroid in the new rotated coordinate system.

Using the substitution $\beta=\theta+\alpha$, $\beta_1=\theta_1+\alpha$, $\beta_2=\theta_2+\alpha$ and $\frac{d\theta}{d\beta}=1$, we have

$\bar{r}'\cos\bar{\theta}'=\bar{x}'=\frac{1}{L}\int_{\beta_1}^{\beta_2}r(\beta)\cos(\beta)\sqrt{r^2(\beta)+(\frac{dr(\beta)}{d\beta})^2}d\beta$

where the primed quantities are the corresponding quantities in the new rotated coordinate system.

Recall that $\bar{r}\cos\bar{\theta}=\frac{1}{L}\int_{\theta_1}^{\theta_2}r(\theta)\cos\theta\sqrt{r^2(\theta)+(\frac{dr(\theta)}{d\theta})^2}d\theta$ is a function of $\theta_1, \theta_2$ and $L$. Let's call it $f=f(\theta_1, \theta_2, L)$. Then

$\bar{r}'\cos\bar{\theta}'=\bar{x}'=f(\beta_1, \beta_2, L)=f(\theta_1+\alpha, \theta_2+\alpha, L)$.

But it remains to show why $\bar{r}'=\bar{r}$ and $\cos\bar{\theta}'=\cos(\bar{\theta}+\alpha)$. That is, why

$f(\theta_1+\alpha, \theta_2+\alpha, L)=\bar{r}\cos(\bar{\theta}+\alpha)$.