Proving one equation, cyclic in variables ##a,b,c##, to another

[brotherbobby]

Homework Statement

Prove the following identity : $\pmb{a^3(b-c)+b^3(c-a)+c^3(a-b) = -(a-b)(b-c)(c-a)(a+b+c)}$

Relevant Equations

I don't know if the following three formulae will be useful, all equivalent to one another and written out in different forms.
1. $ab(a-b)+bc(b-c)+ca(c-a) = -(a-b)(b-c)(c-a)$
2. $a^2(b-c)+b^2(c-a)+c^2(a-b)=-(a-b)(b-c)(c-a)$
3. $a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)= (a-b)(b-c)(c-a)$

Problem statement : Let me copy and paste the problem statement from the text :

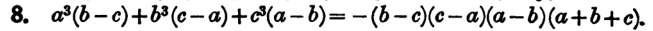
Attempt at solution : I could not solve the problem reducing the L.H.S into the R.H.S. However, I could solve the problem by expanding the R.H.S. into the L.H.S., though it is less than satisfactory. Below is my attempt.

Expanding the R.H.S.
$=-(a-b)(b-c)(c-a)(a+b+c) = (-bc+c^2+ab-ac)(a^2-\cancel{ab}+\cancel{ab}-b^2+ac-bc)= (c^2+ab-bc-ac)(a^2-b^2+ac-bc)$
$=\cancel{a^2c^2}+a^3b-\bcancel{a^2bc}-a^3c-\cancel{b^2c^2}-ab^3+b^3c+\xcancel{ab^2c}+ac^3+\bcancel{a^2bc}-\xcancel{abc^2}-\cancel{a^2c^2}-bc^3-\xcancel{ab^2c}+\cancel{b^2c^2}+\xcancel{abc^2}$
$= a^3(b-c)+b^3(c-a)+c^3(a-b)$. $\Huge{\mathbf{\checkmark}}$

Issue : I have solved the problem, but in an unsatisfactory way, expanding the R.H.S to the L.H.S.

Does anyone know to reduce the L.H.S to the R.H.S, which is the proper way to solve the problem?

A hint or suggestion will be welcome.

 

[anuttarasammyak]

We assume LHS is divisible by (a-b),(b-c) and (c-a) so let us see it,
LHS=(a-b)[c^3-c(a^2+ab+b^2)+ab(a+b)]=(a-b)[c^3-c(a+b)^2+ab(a+b+c)]=(a-b)(a+b+c)[c(c-a-b)+ab]
and so on.

 

[brotherbobby]

We assume LHS is divisible by (a-b),(b-c) and (c-a) so let us see it,
LHS=(a-b)[c^3-c(a^2+ab+b^2)+ab(a+b)]=(a-b)[c^3-c(a+b)^2+ab(a+b+c)]=(a-b)(a+b+c)[c(c-a-b)+ab]
and so on.

I do not get your last expression when I divide the expression by $(a-b)$. I copy and paste my work below. Sorry if the font is too too small.

 

[PeroK]

I don't think there was anything wrong with cranking out a solution. You could, however, notice that the LHS is $0$ whenever $a = b, b = c$ or $a = c$, hence $a-b, b-c$ and $c-a$ are all factors.

Then you could notice that every term on the LHS has order $4$ in $a, b, c$, so we must have a final factor that is linear in $a, b, c$.

Finally, notice that, in particular, $a^3b$ has coefficient of $1$ on the LHS. And, the coefficient of $a^2b$ in $(a-b)(b-c)(c-a)$ is $-1$. The final linear factor in $a$ must be $-1$; and by symmetry be $-1$ for $b$ and $c$ as well.

 

[brotherbobby]

Excellent @PeroK and thank you. I should have known better and used the so-called Factor Theorem at once. While you have literally solved the whole problem with your hints, I'd still like to carry out the last bit myself by explicit division after factoring out $(a-b),(b-c)\;\text{and}\;(c-a)$ terms.