- #1
DaalChawal
- 87
- 0
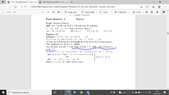
I am confused in (iia) and (iib).
If $x^4 +( \alpha - 1) x^2 + \alpha + 2 = 0$ has real roots that means $y^2 + ( \alpha -1) + \alpha + 2 =0 $ should have at least one non-negative root. This means product of roots of (2) can be greater or less than zero...But I'm not able to comment on sum of roots.
Help Please.