- #1
PainterGuy
- 940
- 69
Hi,
I was watching a video on the origin of Taylor Series shown at the bottom.
Question 1:
The following screenshot was taken at 2:06.
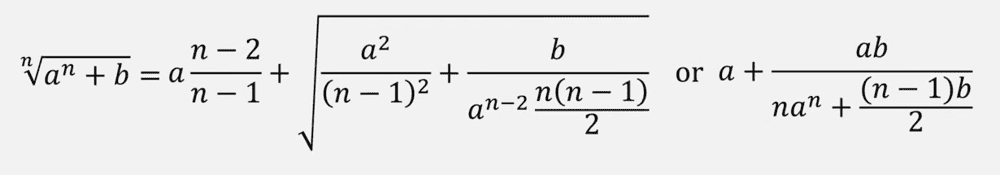
The following is said between 01:56 - 02:05:
Halley gives these two sets of equations for finding nth roots which we can generalize coming up with one irrational and one rational form.
Why are two forms, rational and irrational, needed? Could you please help me with it?Question 2:
The following screenshot was taken at 2:25.

The following is said between 01:56 - 02:24.
Halley gives these two sets of equations for finding nth roots which we can generalize coming up with one irrational and one rational form. Let's look at the irrational. Let's use our earlier example of 1337 and we'll still use the values of eleven and six for a and b. Plug everything in. We get this number. Now we can repeat the calculation using that number for a and whatever would be the remainder we call b. Plug everything in. We get this number which is accurate to fifteen digits.
I don't see how the author comes up with b=0.00000449553611. Also, 1337 ≠ {11.0165041631289^3 + 0.00000449553611}. Could you please help me with it? Thank you!
I was watching a video on the origin of Taylor Series shown at the bottom.
Question 1:
The following screenshot was taken at 2:06.
The following is said between 01:56 - 02:05:
Halley gives these two sets of equations for finding nth roots which we can generalize coming up with one irrational and one rational form.
Why are two forms, rational and irrational, needed? Could you please help me with it?Question 2:
The following screenshot was taken at 2:25.
The following is said between 01:56 - 02:24.
Halley gives these two sets of equations for finding nth roots which we can generalize coming up with one irrational and one rational form. Let's look at the irrational. Let's use our earlier example of 1337 and we'll still use the values of eleven and six for a and b. Plug everything in. We get this number. Now we can repeat the calculation using that number for a and whatever would be the remainder we call b. Plug everything in. We get this number which is accurate to fifteen digits.
I don't see how the author comes up with b=0.00000449553611. Also, 1337 ≠ {11.0165041631289^3 + 0.00000449553611}. Could you please help me with it? Thank you!
