Rings of Fractions .... Lovett, Section 6.2, Proposition 6.2

[Math Amateur]

I am reading Stephen Lovett's book, "Abstract Algebra: Structures and Applications" and am currently focused on Section 6.2: Rings of Fractions ...

I need some help with the proof of Proposition 6.2.6 ... ... ...

Proposition 6.2.6 and its proof read as follows:

In the above proof by Lovett we read the following:

" ... ... By Lemma 6.2.5, the function $\phi$ is injective, so by the First Isomorphism Theorem, $R$ is isomorphic to $\text{Im } \phi$. ... ... "*** NOTE *** The function $\phi$ is defined in Lemma 6.2.5 which I have provided below ... ..
My questions are as follows:Question 1

I am unsure of exactly how the First Isomorphism Theorem establishes that $R$ is isomorphic to $\text{Im } \phi$.

Can someone please show me, rigorously and formally, how the First Isomorphism Theorem applies in this case ...Question 2

I am puzzled as to why the First Isomorphism Theorem is needed in the first place as $\phi$ is an injection by Lemma 6.2.5 ... and further ... obviously the map of $R$ to $\text{Im } \phi$ is onto, that is a surjection ... so $R$ is isomorphic to $\text{Im } \phi$ ... BUT ... why is Lovett referring to the First Isomorphism Theorem ... I must be missing something ... hope someone can clarify this issue ...Hoe that someone can help ... ...

Peter===================================================

In the above, Lovett refers to Lemma 6.2.5 and the First Isomorphism Theorem ... so I am providing copies of both ...Lemma 6.2.5 reads as follows:

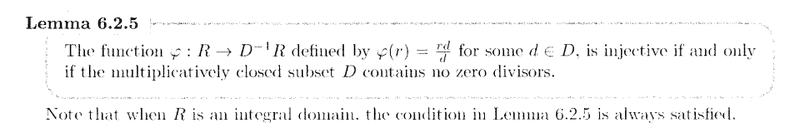
The First Isomorphism Theorem reads as follows:

 

[willem2]

question1.
since φ is injective, Ker φ only contains the identity of R, so R is isomorphic to φ(R) = I am φ according to the isomorphism theorem.
question2.
no Idea. You can easily see that φ i a bijection, so R must be isomorphic to I am φ.

 

[Math Amateur]

question1.
since φ is injective, Ker φ only contains the identity of R, so R is isomorphic to φ(R) = I am φ according to the isomorphism theorem.
question2.
no Idea. You can easily see that φ i a bijection, so R must be isomorphic to I am φ.

Hi willem2,

Thanks for the help ...

Yes, I can see the main thread of your argument ...

... basically ...

$\phi injective$

$\Longrightarrow \text{Ker } \phi = {0}$ ... ... that is $\text{Ker } \phi$ contains only additive identity of R

$\Longrightarrow R/ \text{Ker } \phi = R/ {0} = R \cong \text{Im } \phi$

Is that correct?... BUT ...

Can you explain in simple terms, why $R/ {0} = R$ ... ...?

Peter

 

[fresh_42]

Can you explain in simple terms, why $R/ {0} = R$

$R/\{0\} = \{r + \{0\}\,\vert \,r \in R\} = \{\{r\}\,\vert \,r \in R\} \cong \{r\,\vert \,r \in R\} = R$.
Did you mean something like this? Remember that $R/I$ is the set of all cosets $r+I$.

 

[Math Amateur]

$R/\{0\} = \{r + \{0\}\,\vert \,r \in R\} = \{\{r\}\,\vert \,r \in R\} \cong \{r\,\vert \,r \in R\} = R$.
Did you mean something like this? Remember that $R/I$ is the set of all cosets $r+I$.

Thanks fresh_42 ... yes, exactly what I meant ...

Would the answer be the same for $R/ \{a \}$ where $a$ was a given particular element of $R$? Indeed what would the various cosets be?

Peter

 

[fresh_42]

You could formally build cosets $r+\{a\}$ but unless you take the ideal generated by $a$, i.e. $Ra$, you won't get a structure of interest on $R/\{a\}$. E.g. if $[x]_a$ denotes the coset $x+\{a\}$, then $[0]_a \neq [a+a]_a$ because $a+a \notin \{a\}$ and on the other hand $[a]_a + [a]_a = [0]_a + [0]_a.$ Thus $[a+a]_a = [a]_a + [a]_a$ cannot be concluded, which means you cannot add anymore unless $a=0$.

So better forget about this idea of cosets of single elements other than zero. At least we want to have a subring; ideal would be better.

If you want to learn something about cosets, you could prove the following as an exercise:
Given a subgroup $U$ of a finite group $G$. Then $G/U$ is well defined and $U$ partitions $G$ into equally large subsets of $G$, the cosets $xU$.
But $G/U$ carries a group structure again, if and only if $U$ is a normal subgroup of $G$.

This is the reason why we consider normal subgroups instead of only subgroups. I haven't done the math, but I assume it's similar with ideals and subrings. So factoring along a single point set only makes sense, if this point is the neutral element of the underlying group. And rings only build a group with addition, because multiplication isn't invertible.

 

[WWGD]

$R/\{0\} = \{r + \{0\}\,\vert \,r \in R\} = \{\{r\}\,\vert \,r \in R\} \cong \{r\,\vert \,r \in R\} = R$.
Did you mean something like this? Remember that $R/I$ is the set of all cosets $r+I$.

I wonder if in a sense we can consider this as an allowable case of division by 0.

 

[fresh_42]

I wonder if in a sense we can consider this as an allowable case of division by 0.

You look like a quotient
Walk like a quotient
Talk like a quotient
But I got wise
You're an addition in disguise
Oh, yes, you are
Addition in disguise

You fooled me with your slashes
You cheated and you schemed
Heaven knows how you lied to me
You're not the way you seemed
...

 

[WWGD]

You look like a quotient
Walk like a quotient
Talk like a quotient
But I got wise
You're an addition in disguise
Oh, yes, you are
Addition in disguise

You fooled me with your slashes
You cheated and you schemed
Heaven knows how you lied to me
You're not the way you seemed
...

Still, you may mod out by a non-Abelian group, in which case it does not come down to addition.