Simple Riemann zeta function algebra help

[tim9000]

Hi

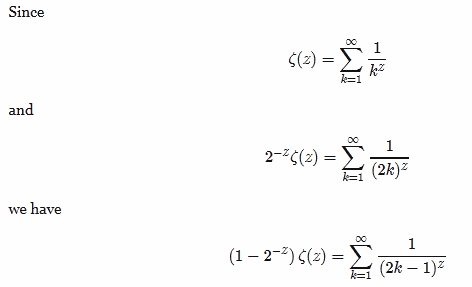
It's just that last step I'm not getting, so you have:
[1 / K^z] - [1 / (2K)^z]
= [ (2K)^z - K^z ] / [(2K)^z * K^z]
= [ (2)^z - 1 ] / [(2K)^z*]
Then what?
Thanks

 

[Mark44]

Hi
View attachment 80246
It's just that last step I'm not getting, so you have:
[1 / K^z] - [1 / (2K)^z]
= [ (2K)^z - K^z ] / [(2K)^z * K^z]
= [ (2)^z - 1 ] / [(2K)^z*]
Then what?
Thanks

Expand the first series, and you get $\frac{1}{1^k} + \frac{1}{2^k} + \frac{1}{3^k} + ... + \frac{1}{n^k} ...$
Expand the second series, and you get $\frac{1}{2^k} + \frac{1}{4^k} + ... + \frac{1}{(2n)^k} ...$
If you subtract the second series from the first, term by term, what do you get?

 

[tim9000]

Expand the first series, and you get $\frac{1}{1^k} + \frac{1}{2^k} + \frac{1}{3^k} + ... + \frac{1}{n^k} ...$
Expand the second series, and you get $\frac{1}{2^k} + \frac{1}{4^k} + ... + \frac{1}{(2n)^k} ...$
If you subtract the second series from the first, term by term, what do you get?

Sorry, I'm not sure, I'm too rusty.

 

[Mark44]

Can you see that every term in the second series is also present in the first series?

 

[tim9000]

Can you see that every term in the second series is also present in the first series?

Ah, I've been trying to use factorisation and cancellation.
So when you minus S1 - S2 it leaves only 1/1^k
but how does that explain the final line of working they got for the sum?

 

[Mark44]

Ah, I've been trying to use factorisation and cancellation.
So when you minus S1 - S2 it leaves only 1/1^k

No, that's not right. You still end up with a series with an infinite number of terms. Every term in the 2nd series is in the first series, but not every term in the 1st series is in the second. Expand both series like I did above, but with more terms, and then do the subtraction.

but how does that explain the final line of working they got for the sum?

 

[mathman]

Sorry, I'm not sure, I'm too rusty.

The second series consists of the reciprocals of powers of even integers. The first series consists of the reciprocals of all integers. Subtract the second from the first leaves the reciprocals of the powers of all odd integers.

 

[tim9000]

No, that's not right. You still end up with a series with an infinite number of terms. Every term in the 2nd series is in the first series, but not every term in the 1st series is in the second. Expand both series like I did above, but with more terms, and then do the subtraction.

The second series consists of the reciprocals of powers of even integers. The first series consists of the reciprocals of all integers. Subtract the second from the first leaves the reciprocals of the powers of all odd integers.

Woops, yes I see what you were saying. Aaah ok, no wonder I couldn't rearrange it, I was contemplating partial fractions etc.
Thanks