Solution of a parametric differential equation

[patric44]

Homework Statement

solution of a parametric equation related to vertical motion

Relevant Equations

D2y = -a-k*(Dy)^3

hi guys
i was trying to solve this differential equation $\frac{d^{2}y}{dt^{2}}=-a-k*(\frac{dy}{dt})^{3}$ in which it describe the motion of a vertical projectile in a cubic resisting medium , i know that this equation is separable in $\dot{y}$ but in order to solve for $y$ it becomes unsolvable in this form , so i came up with this parametric solution

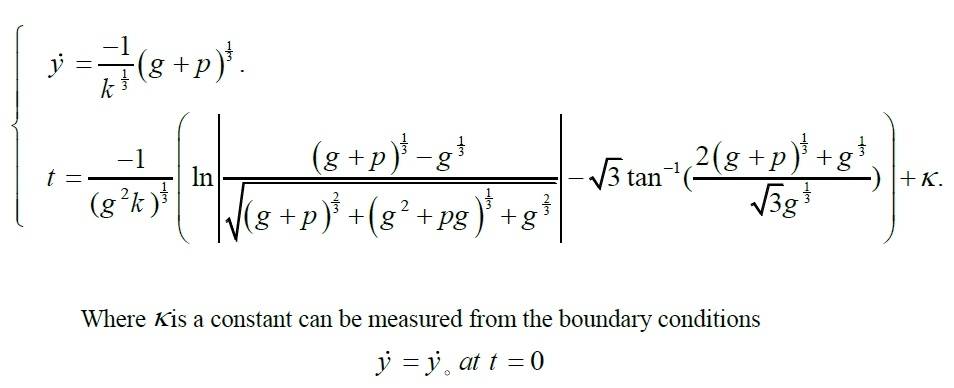
and i would like to solve this parametric differential equation for $y$ but don't know what is the approach for it
i will appreciate any help , thanks

 

[William Crawford]

...i was trying to solve this differential equation $\frac{d^{2}y}{dt^{2}}=-a-k*(\frac{dy}{dt})$ ...

Your ODE is a second-order linear equation with constant coefficients. It is rather straightforward to solve, simply observe that you can write it in the following form
$$ \big(e^{kt}y^\prime\big)^\prime = - ae^{kt}.$$
Now you simply have to integrate twice.

 

[patric44]

Your ODE is a second-order linear equation with constant coefficients. It is rather straightforward to solve, simply observe that you can write it in the following form
(ekty′)′=−aekt.
Now you simply have to integrate twice.

i am sorry i meant to write $(\frac{dy}{dt})^3$ . its not very simple in this case

 

[William Crawford]

i am sorry i meant to write $(\frac{dy}{dt})^3$ . its not very simple in this case

No worries! It was me that read your original post in a hurry. Your differential equation in $y^\prime$ belong to a notorious difficult class of ODE's called Abel's nonlinear ODE's of the fist-kind. I haven't had the change nor time to study this class of ODE's, so I'm afraid that I can't provide you with any hint to how to selve it (if possible).
Is this homework?

 

[docnet]

just for kicks, i put the ODE into mathematica and got $$\left\{\left\{y(t)\to \frac{2 \log \left(\sqrt[3]{a}+\sqrt[3]{k} \text{InverseFunction}\left[-\frac{\log \left(\text{$\#$1}^2 k^{2/3}+\text{$\#$1} \left(-\sqrt[3]{a}\right) \sqrt[3]{k}+a^{2/3}\right)-2 \log \left(\text{$\#$1} \sqrt[3]{k}+\sqrt[3]{a}\right)+2 \sqrt{3} \tan ^{-1}\left(\frac{1-\frac{2 \text{$\#$1} \sqrt[3]{k}}{\sqrt[3]{a}}}{\sqrt{3}}\right)}{6 a^{2/3} \sqrt[3]{k}}\&\right][-t+c_1]\right)-\log \left(-\sqrt[3]{a} \sqrt[3]{k} \text{InverseFunction}\left[-\frac{\log \left(\text{$\#$1}^2 k^{2/3}+\text{$\#$1} \left(-\sqrt[3]{a}\right) \sqrt[3]{k}+a^{2/3}\right)-2 \log \left(\text{$\#$1} \sqrt[3]{k}+\sqrt[3]{a}\right)+2 \sqrt{3} \tan ^{-1}\left(\frac{1-\frac{2 \text{$\#$1} \sqrt[3]{k}}{\sqrt[3]{a}}}{\sqrt{3}}\right)}{6 a^{2/3} \sqrt[3]{k}}\&\right][-t+c_1]+k^{2/3} \text{InverseFunction}\left[-\frac{\log \left(\text{$\#$1}^2 k^{2/3}+\text{$\#$1} \left(-\sqrt[3]{a}\right) \sqrt[3]{k}+a^{2/3}\right)-2 \log \left(\text{$\#$1} \sqrt[3]{k}+\sqrt[3]{a}\right)+2 \sqrt{3} \tan ^{-1}\left(\frac{1-\frac{2 \text{$\#$1} \sqrt[3]{k}}{\sqrt[3]{a}}}{\sqrt{3}}\right)}{6 a^{2/3} \sqrt[3]{k}}\&\right][-t+c_1]{}^2+a^{2/3}\right)+2 \sqrt{3} \tan ^{-1}\left(\frac{1-\frac{2 \sqrt[3]{k} \text{InverseFunction}\left[-\frac{\log \left(\text{$\#$1}^2 k^{2/3}+\text{$\#$1} \left(-\sqrt[3]{a}\right) \sqrt[3]{k}+a^{2/3}\right)-2 \log \left(\text{$\#$1} \sqrt[3]{k}+\sqrt[3]{a}\right)+2 \sqrt{3} \tan ^{-1}\left(\frac{1-\frac{2 \text{$\#$1} \sqrt[3]{k}}{\sqrt[3]{a}}}{\sqrt{3}}\right)}{6 a^{2/3} \sqrt[3]{k}}\&\right][-t+c_1]}{\sqrt[3]{a}}}{\sqrt{3}}\right)}{6 \sqrt[3]{a} k^{2/3}}+c_2\right\}\right\}$$