- #1
iZnoGouD
- 2
- 0
can you explain why this happen? i can't understand
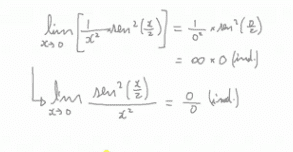
thks in advance
thks in advance
Levex said:I still don't understand why people want to divide by zero. It's completely nonsense...
algebrat said:You're not actually dividing by zero. You come close to dividing by zero, never do, and the ratios of the two functions that are heading to zero, that ratio may actually head towards a well-defined number.
Sorry to burst your "ooh, there's a rip in the space-time continuum" bubble.
daniel.e2718 said:This is true. But we are talking about limits, so I figured that that was implied.
Solving math doubt is important because it helps us understand concepts and principles of mathematics, which are essential in many fields such as science, engineering, and finance. It also improves critical thinking skills and problem-solving abilities.
To solve a math doubt, it is important to first identify the specific concept or problem that is causing confusion. Then, review related materials such as lecture notes, textbooks, or online resources to gain a better understanding. If needed, seek help from a teacher or tutor.
Math doubts can arise from a variety of reasons, including lack of understanding of fundamental concepts, not paying attention in class, or rushing through problems without fully comprehending the steps. It can also be caused by anxiety or fear of math.
To prevent future math doubts, it is important to actively engage in class, take thorough notes, and practice regularly. It is also helpful to ask questions and seek clarification when needed. Additionally, developing good study habits and seeking help when needed can prevent future math doubts.
Yes, there are many resources available to help you solve math doubts. These include textbooks, online tutorials, practice problems, and study groups. Your teacher or tutor can also provide guidance and assistance in solving math doubts.