Special Relativity & Lorentz Transformation Q: Clock C2 Reading?

[alan123hk]

I believe this does not belong to the homework category. I hope I won't be mistaken.

I am reading a book to self-study special relativity, the following is an example mentioned in the book.

When clock C' and clock C1 meet at times t'=t1=0, both clocks read zero. The Observer in reference frame S determines that the readings of the C1 clock and the C2 clock are the same because they are precisely aligned with each other. However, for the observer in the reference frame S', the two clocks C1 and C2 are not synchronized, when the reading of C1 is 0, the reading of C2 is not zero. Assume that the moving speed of the reference frame S' in the positive x direction relative to the reference frame S is v. The distance between C1 and C2 measured by the observer in the reference frame S is L. So when C' and C1 meet at time t'= t1=0, how does the observer in the reference frame S' think of the reading (Δ) of the clock C2 ?

​

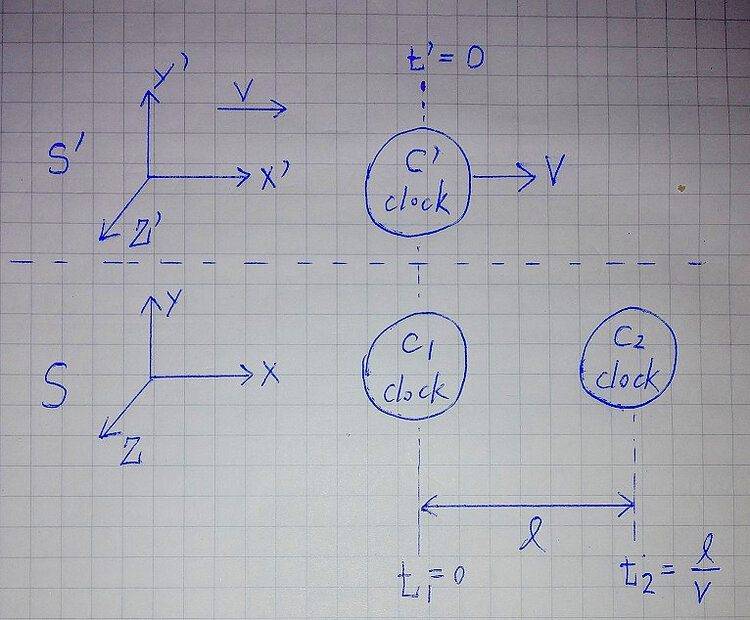
The answer mentioned in the book is to use the Lorentz transformation formula, as shown below.

$$ t' = \gamma \left( t-\frac {v} {c^2} x \right) ~~~~~\Rightarrow~~~~~t'=0= \gamma \left( \Delta-\frac {v} {c^2} L \right)~~~~~\Rightarrow~~~~~\Delta=\frac {v} {c^2}L $$

But unfortunately I don't understand the above reasoning logic. Is the above answer correct ?

I may be wrong, but I feel that the following way is more reasonable.

$$ t' = \gamma \left( t-\frac {v} {c^2} x \right) ~~~~~\Rightarrow~~~~~t'=\Delta= \gamma \left(0-\frac {v} {c^2} L \right)~~~~~\Rightarrow~~~~~\Delta=-\gamma\frac {v} {c^2}L $$
This seems to be really wrong, why dose the answer have a minus sign.
What is wrong with my derivation process above ?

Thanks for helping.

 

[PeroK]

I am reading a book to self-study special relativity, the following is an example mentioned in the book.

When clock C' and clock C1 meet at times t'=d t1=0, both clocks read zero.

You've lost me here. What does $t' = d$ mean?

After that I can see a question - which is to calculate the loss of synchronisation of clocks $C_1$ and $C_2$ in the primed frame. But, I don't see a derivation of that.

 

[PeroK]

PS unless you simply hit this problem with the Lorentz Transformation, then you have to be very careful not to go wrong. Juggling time dilation, length contraction and the relative motion requires a cool head!

 

[alan123hk]

You've lost me here. What does t′=d mean?

Typo, Now corrected

But, I don't see a derivation of that.

I have a problem dealing with the LaTeX for Math Equations and the derivation process should now be displayed .

 

[PeroK]

The answer mentioned in the book is to use the Lorentz transformation formula, as shown below.

t′=γ(t−vc2x) ⇒ t′=0=γ(Δ−vc2x) ⇒ Δ=vc2L

But unfortunately I don't understand the above reasoning logic. Is the above answer correct ?

Okay, there's a conceptual issue here. (Is this book Taylor and Wheeler? )

The Lorentz Transformation (LT) is a transformation between reference frames - each of which has coordinates for every point in spacetime. It's not relating what different individual observers record, but rather the relationship between coordinates in different reference frames. In that sense it is a mathematical calculation that can be carried out without direct reference to specific moving clocks and whatever.

If we want to understand the LT in this case, we must imagine a row of clocks in the primed frame, all synchronised. When the clock C' is at the origin it reads t' = 0. We have another clock C'_2, say, that reads t' = 0 when it passes clock C_2. (In this frame C_2 is coming in from the right and must be somewhere at t′=0.

The question is: what does clock C2 read at t′=0? And that, using the LT, is $+\frac{vL}{c^2}$

That explains what the book is doing. I'll do another post shortly looking at your derivation.

 

[PeroK]

Actually, let me say a bit more about what the LT is doing here. First, we are going to look at the coordinates of the clocks $C_1$ and $C_2$ as seen in the primed frame.

We know that clock $C_1$ is at $x' = 0$ at $t' = 0$ and that it reads $t = 0$ for that event. That's all we need to know.

We know that clock $C_2$ is fixed at coordinate $x = L$ in frame $S$. So, it's coordinates in frame $S$ are $(t, L)$, where $t$ is a variable here. Using the LT we get the coordinates of $C_2$ in frame $S'$. These are:$$(\gamma(t - \frac{vL}{c^2}), \gamma(L - vt))$$In a way, that's not much use, because we want to know about $C_2$ at $t' =0$. So, we need to set $t' = 0$ here. That means we need $$t = +\frac{vL}{c^2}$$ In other words, when we transform the event $(\frac{vL}{c^2}, L)$ (which is where $C_2$ is when it reads $t = \frac{vL}{c^2}$, we get the primed coordinates:
$$(0, \gamma(L - \frac{v^2L}{c^2}))$$ And that's where $C_2$ is at $t' = 0$ in $S'$. For this exercise, we don't need to know where it is at $t' = 0$, but we have established that it reads $t = \frac{vL}{c^2}$.

And, this compares with clock $C_1$, which reads $t = 0$ at $t' = 0$ and gives us the loss of synchronisation of clocks $C_1, C_2$ in the primed frame.

 

[PeroK]

Actually, let me just finish this off by summarising everything. Using the LT, we find that at $t' = 0$ in the primed frame:

Clock $C_1$ is at $x' = 0$ and reads $t = 0$.

Clock $C_2$ is at $x' = \frac L \gamma$ and reads $t = +\frac{vL}{c^2}$.

 

[PeroK]

I may be wrong, but I feel that the following way is more reasonable.

$$ t' = \gamma \left( t-\frac {v} {c^2} x \right) ~~~~~\Rightarrow~~~~~t'=\Delta= \gamma \left(0-\frac {v} {c^2} L \right)~~~~~\Rightarrow~~~~~\Delta=-\gamma\frac {v} {c^2}L $$
This seems to be really wrong, why dose the answer have a minus sign.
What is wrong with my derivation process above ?

Let's figure out what you've calculated here. You have transformed the coordinates of the event $(0, L)$ (that's clock C_2 at time $t = 0$) into the primed frame and (correctly) got $t ' = -\gamma\frac {v} {c^2}L$.

In other words, at $t' = -\gamma\frac {v} {c^2}L$, clock $C_2$ reads $t = 0$. This isn't quite what we want. We really wanted to know what clock $C_2$ reads at $t' = 0$.

You can rescue this calculation by running time $t'$ forward and using time dilation for clock $C_2$ to conlcude that, as above:

At time $t' = 0$, clock $C_2$ will read $$t = 0 + \frac 1 \gamma (\gamma\frac {v} {c^2}L) = \frac {v} {c^2}L$$

 

[alan123hk]

Let's figure out what you've calculated here. You have transformed the coordinates of the event (0,L) (that's clock C_2 at time t=0) into the primed frame and (correctly) got t′=−γvc2L.

In other words, at t′=−γvc2L, clock C2 reads t=0. This isn't quite what we want. We really wanted to know what clock C2 reads at t′=0.

You can rescue this calculation by running time t′ forward and using time dilation for clock C2 to conlcude that, as above:

At time t′=0, clock C2 will read

Thanks for your help.

I need time to digest and understand the rich content you provide. It seems that even a seemingly simple special relativity problem is still a complicated logical problem for me. I feel a little confused now.

Please give me time, I hope I can fully understand everything you say.

 

[alan123hk]

I feel that I am beginning to understand some things, but there seems to be a lot of doubts. I want to ask another question that I can't figure out.

The event in the S frame is $S(t=\frac{vL}{c^2},~x=L)$
The observer in S' frame think this happen at $S'\left(t'=0, ~x'=\gamma(L - \frac{v^2L}{c^2}) \right)$

If my understanding is correct, it can be said that the observer in reference frame S' at time zero and location $\gamma(L - \frac{v^2L}{c^2})$ can see the clock C2 of reference frame S is actually display as $\frac{vL}{c^2}$

But if according to this reasoning method, the event that occurred in the reference frame S includes two elements $~ \left( t=\frac{vL}{c^2} \right) ~$and$~ \left(x=L \right)$, then how do the observer in reference frame S' understand or measure the parameter $L$ ? Should he ignore it or not be able to read this parameter?

For time $~\left( \frac{vL}{c^2} \right)~$, this should be no problem, because the observer in reference frame S' can read the real clock C2 placed in reference frame S, but how does he determine the $( L)$, and this $(L)$ in reference frame S seems to be contradict to his own $\left( \gamma(L - \frac{v^2L}{c^2} \right)$ in reference frame S'

 

[PeroK]

The event in the S frame is $S(t=\frac{vL}{c^2},~x=L)$
The observer in S' frame think this happen at $S'(t'=0, ~x'=\gamma(L - \frac{v^2L}{c^2})$

If my understanding is correct, it can be said that the observer in reference frame S' at time zero and location $\gamma(L - \frac{v^2L}{c^2})$ can see the clock C2 of reference frame S is actually display as $\frac{vL}{c^2}$

Yes, that's precisely what the LT is telling us. I would replace "thinks" by "measures".

But if according to this reasoning method, the event that occurred in the reference frame S includes two elements $~ \left( t=\frac{vL}{c^2} \right) ~$and$~ \left(x=L \right)$, then how do the observer in reference frame S' understand or measure the parameter $L$ ?

In the reference frame $S'$, the two clocks ($C_1$ and $C_2$) are moving with equal velocity $v$, a fixed distance of $\frac L \gamma$ apart. This is simply length contraction. Additionally, the clocks are measured to be running slow ($\gamma \Delta t$ = $\Delta t'$, as measured in $S'$). That's time dilation. And, they are out of synchronisation (by a fixed time difference of $\frac{vL}{c^2}$). That's the relativity of simultaneity.

Note that all of those things may be derived directly and this serves as a test that confirms the LT in this respect.

For time $~\left( \frac{vL}{c^2} \right)~$, this should be no problem, because the observer in reference frame S' can read the real clock C2 placed in reference frame S, but how does he determine the $( L)$, and this $(L)$ in reference frame S seems to be contradict to his own $\left( \gamma(L - \frac{v^2L}{c^2} \right)$ in reference frame S'

That expression simplifies to:
$$( \gamma(L - \frac{v^2L}{c^2}) = \gamma L(1 - \frac{v^2}{c^2}) = \gamma L(\frac{1}{\gamma^2}) = \frac{L}{\gamma}$$Which is the expected length contraction of the fixed distance between the clocks.

 

[alan123hk]

I think that since the observer in the reference frame S' can see that the C2 of reference frame S shows that the time reading $(\frac{vL}{c^2})$ is different from his own $(zero)$, then he should also be able to see that the distance value $(L)$ of the C2 from the origin in the reference S is also different from the distance value $( \frac {L} {\gamma})$ measured by himself.

So I believe that if a long ruler is placed in the reference frame S, the observer in S' will find that this long ruler will also appear at the same position $( \frac {L} {\gamma})$ of C2 in reference S', but the scale on the ruler still shows that the position of C2 is $L$ instead of $( \frac {L} {\gamma})$

If my concept is wrong, please let me know

 

[PeroK]

So I believe that if a long ruler is placed in the reference frame S, the observer in S' will find that this long ruler will also appear at the same position $( \frac {L} {\gamma})$ of C2 in reference S', but the scale on the ruler still shows that the position of C2 is $L$ instead of $( \frac {L} {\gamma})$

If my concept is wrong, please let me know

That's simply length contraction. If the ruler has length $L$ in frame $S$ and measures the fixed distance between $C_1$ and $C_2$ in that frame, then it has length $\frac L \gamma$ in frame $S'$ and measures the fixed distance between $C_1$ and $C_2$ in that frame.