- #1
Simpl0S
- 14
- 0
In Spivak's Calculus, on page 121 there is this theorem
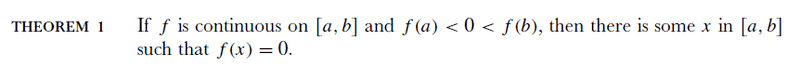
Then he generalizes that theorem:
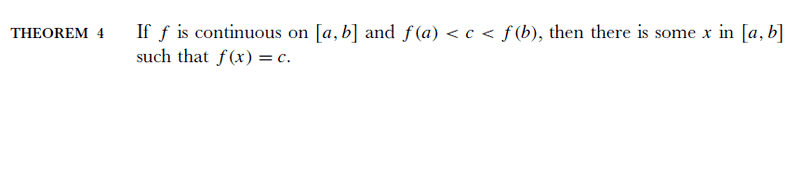
I tried proving theorem 4 on my own, before looking at Spivak's proof. Thus I let c = 0 and then by theorem 1, my proof would be completed. Is this a correct proof?
Spivak's proof for theorem 4:
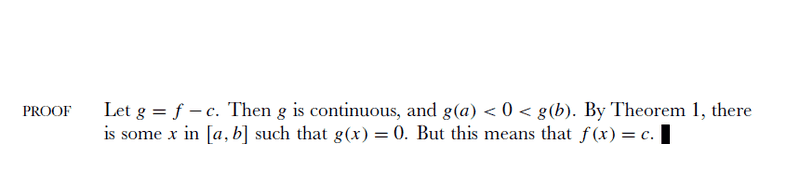
And also can someone explain to me the choice of why Spivak has chosen the equation g = f - c. I understand his proof but the choice would have never occurred to me intuitively.
Then he generalizes that theorem:
I tried proving theorem 4 on my own, before looking at Spivak's proof. Thus I let c = 0 and then by theorem 1, my proof would be completed. Is this a correct proof?
Spivak's proof for theorem 4:
And also can someone explain to me the choice of why Spivak has chosen the equation g = f - c. I understand his proof but the choice would have never occurred to me intuitively.