Stress-energy tensor definition

[coleman123]

I have seen two definitions with oposite signs (for one of the pressure terms in the formula) all over the web and books. I suspect it is related to the chosen metric signature, but I found no references to that.

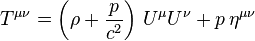
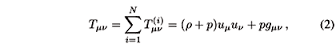
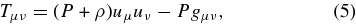
General Relativity An Introduction for Physicists from M. P. HOBSON, G. P. EFSTATHIOU and A. N. LASENBY uses a negative sign.

Wald uses a positive sign..

And so on..

What's happening?

 

[Mentz114]

I don't think the signature matters. Stephani uses a + sign like your first example. I always used this form so it looks as if H, E & L are in a minority.

 

[Bill_K]

The coefficient of P is a projection operator into the 3-space orthogonal to u^μ. If you use η^μν = (1, -1, -1, -1) it should be u^μu^ν - η^μν, while if you use η^μν = (-1, 1, 1, 1) it should be u^μu^ν + η^μν.

 

[Mentz114]

The coefficient of P is a projection operator into the 3-space orthogonal to u^μ. If you use η^μν = (1, -1, -1, -1) it should be u^μu^ν - η^μν, while if you use η^μν = (-1, 1, 1, 1) it should be u^μu^ν + η^μν.

I guess that sorts out the issue.

 

[coleman123]

The coefficient of P is a projection operator into the 3-space orthogonal to u^μ. If you use η^μν = (1, -1, -1, -1) it should be u^μu^ν - η^μν, while if you use η^μν = (-1, 1, 1, 1) it should be u^μu^ν + η^μν.

Thanks Bill. So the metric matters then. In the end I was just using:

T^μν=(ρ+P/c²)u^μu^ν-sPg^μν

where "s" is the sign corresponding to the time coordinate.

Where do I find more about this?

Thank you

 

[Bill_K]

I'm not sure what you're looking for, but there's an online treatment of relativistic fluid dynamics http://relativity.livingreviews.org/open?pubNo=lrr-2007-1&page=articlese6.html that's rather complete.

 

[coleman123]

That's it. Thanks again

 

[coleman123]

To enrich this topic a little more (not mine):

http://equatorfreq.wordpress.com/2010/08/13/signs-in-einsteins-equation/