- #1
JVNY
- 153
- 2
Here for your consideration is a try at synchronizing clocks on a rim rotating at a constant angular velocity. It is restricted to two clocks, each at the opposite end of a diameter of the rim.
It is based on simultaneity as determined in SR. Taylor and Wheeler in Spacetime Physics, page 120, referring to two inertial frames (rocket and lab), state regarding simultaneity:
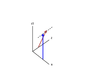
If at that instant one sets the two clocks to the same time, they will agree that the setting is simultaneous, and the clocks will be for that instant synchronized. The first diagram attached shows the world lines of two objects in inertial motion and the instant that they agree on simultaneity (at the dashed line).
Clocks at opposite ends of a diameter have instantaneous velocity tangent to the rim, so they have instantaneous velocity in opposite directions, perpendicular to the diameter. See a diagram from wikipedia at http://en.wikipedia.org/wiki/File:Uniform_circular_motion.svg or previously posted here at post 3, https://www.physicsforums.com/showthread.php?t=730574#post4616303.
Therefore, at any instant the two clocks agree on simultaneity of events that occur along the line perpendicular to their relative motion. That is, they agree on the simultaneity of events that occur along the diameter. Therefore one can synchronize them using synchronized clocks that are at rest underneath them (say in the lab frame in which the rim is rotating). As the rotating clocks pass over the synchronized lab clocks, the rotating clocks are set to the time shown on the lab clocks.
Subsequently, the rim clocks travel at all times with velocity perpendicular to the diameter. So they continue to agree on simultaneity. So they remain synchronized.
For a more detailed discussion of the relationship between simultaneity and synchronization, see: https://www.physicsforums.com/showthread.php?t=731437
For an earlier discussion of the proposed synchronization method, see:
https://www.physicsforums.com/showthread.php?t=730574
It is based on simultaneity as determined in SR. Taylor and Wheeler in Spacetime Physics, page 120, referring to two inertial frames (rocket and lab), state regarding simultaneity:
At any instant there is just one plane in which both the laboratory and the rocket clocks agree . . . [T]his plane lies perpendicular to the direction of relative motion.
If at that instant one sets the two clocks to the same time, they will agree that the setting is simultaneous, and the clocks will be for that instant synchronized. The first diagram attached shows the world lines of two objects in inertial motion and the instant that they agree on simultaneity (at the dashed line).
Clocks at opposite ends of a diameter have instantaneous velocity tangent to the rim, so they have instantaneous velocity in opposite directions, perpendicular to the diameter. See a diagram from wikipedia at http://en.wikipedia.org/wiki/File:Uniform_circular_motion.svg or previously posted here at post 3, https://www.physicsforums.com/showthread.php?t=730574#post4616303.
Therefore, at any instant the two clocks agree on simultaneity of events that occur along the line perpendicular to their relative motion. That is, they agree on the simultaneity of events that occur along the diameter. Therefore one can synchronize them using synchronized clocks that are at rest underneath them (say in the lab frame in which the rim is rotating). As the rotating clocks pass over the synchronized lab clocks, the rotating clocks are set to the time shown on the lab clocks.
Subsequently, the rim clocks travel at all times with velocity perpendicular to the diameter. So they continue to agree on simultaneity. So they remain synchronized.
For a more detailed discussion of the relationship between simultaneity and synchronization, see: https://www.physicsforums.com/showthread.php?t=731437
For an earlier discussion of the proposed synchronization method, see:
https://www.physicsforums.com/showthread.php?t=730574