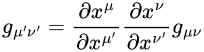Taylor Expansion of Metric Transformation in RNCs

[chartery]

TL;DR Summary

Trouble following sketch proof !

Carroll expands both sides of metric transformation (Notes eq2.35, Book eq2.48)

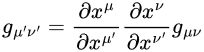to equate powers of x’.

He starts with eq2.36 (2.49):

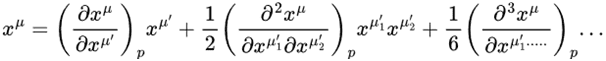
So far so good, though I feel my understanding of multivariable Taylor series starting to struggle.

He refers to Schutz for details, where I find eq 6.23:

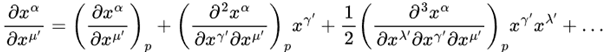
It seems to me that applying

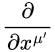to 2.36 should give a version of 6.23, but the constant coefficients seem offset?

Then the left hand side of Carroll 2.37 agrees with Schutz 6.24, but trying to understand the right hand side, I find Schutz 6.26 with too many indices and Carroll 2.37 too few, for me to follow.

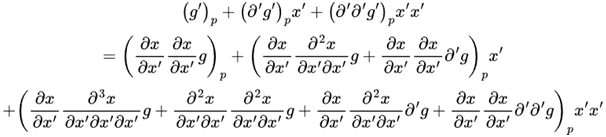
The presence of partial derivatives of g imply some application of the product rule which I don’t understand, when (I presume) substituting the two Taylor expansions. Or am I completely off-piste? :-)

 

[strangerep]

View attachment 327322
So far so good, though I feel my understanding of multivariable Taylor series starting to struggle.

Note that Carroll assumes $x^\mu(p) = x^{\mu'}(p) = 0$, otherwise there would be a $x^{\mu'}(p)$ at the start of the RHS.

He refers to Schutz for details,

I must have a different edition of Schutz than you. Mine involves $\Lambda^\alpha_{~\mu'}$, but that's just $\partial x^\alpha/\partial x^{\mu'}$, so I guess it's the same.

where I find eq 6.23:

View attachment 327324It seems to me that applying View attachment 327325 to 2.36 should give a version of 6.23, but the constant coefficients seem offset?

Note that one formula is an expansion of $x^\mu(p)$ while the other is an expansion of $\Lambda^\alpha_{~\mu'} = \partial x^\alpha/\partial x^{\mu'}$. That's what makes the numerical coefficients seem offset (but in fact they're correct.

If this is still not clear, try writing out the first few terms of an expansion of $\Lambda^\alpha_{~\mu'}$ as if you didn't know it's a partial derivative.

Then the left hand side of Carroll 2.37 agrees with Schutz 6.24, but trying to understand the right hand side, I find Schutz 6.26 with too many indices and Carroll 2.37 too few, for me to follow.

View attachment 327326

The presence of partial derivatives of g imply some application of the product rule which I don’t understand, when (I presume) substituting the two Taylor expansions. Or am I completely off-piste? :-)

There's no differentiation going on to get Carroll's (2.50) [Book]. It's just multiplying 3 expansions (2 for the partial derivatives and 1 for g), then collecting coefficients of each power of $x$.

If that's still not clear, try writing out the expansion of $g_{\mu\nu}$ separately. Then also write out the expansion of $\partial x^\alpha/\partial x^{\mu'}$ as an expansion of $\Lambda^\alpha_{~\mu'}$ instead. Maybe just keep the first 2 terms in each to start with -- so you can see more easily what happens when you multiply all 3 expansion expressions.

HTH.

 

[chartery]

@strangerep, many thanks.

Yes, I 'translated' the Schutz.The coefficient offset arises when:

which would give coefficient 1/2 to the single power of $x^{\mu'}$ whereas Schutz 6.23 has 1/2 on the second power?Also, I thought $g^{'}_{\mu\nu}\left( x' \right)$ would imply $g_{\mu\nu}\left( x \right)$,and so the latter would not need expansion in x' ?

 

[strangerep]

Also, I thought $g^{'}_{\mu\nu}\left( x' \right)$ would imply $g_{\mu\nu}\left( x \right)$,and so the latter would not need expansion in x' ?

Look at Carroll's eq(2.48)[book]. He writes $$ g_{\hat\mu \hat\nu} ~=~ \frac{\partial x^\mu}{\partial x^{\hat\mu}} \; \frac{\partial x^\nu}{\partial x^{\hat\nu}} \; g_{\mu\nu} ~,$$but it should really be written as
$$g_{\hat\mu \hat\nu}(\hat x) ~=~ \frac{\partial x^\mu}{\partial x^\hat\mu}\; \frac{\partial x^\nu}{\partial x^\hat\nu} \; g_{\mu\nu}(x) ~,$$to show the variable dependence explicitly.

Thus, in your notation, i.e., $g'_{\mu\nu}(x' )$ should be interpreted to mean "transform not only the components of the tensor $g$, but also the variable on which it depends".

 

[chartery]

Thus, in your notation, i.e., $g'_{\mu\nu}(x' )$ should be interpreted to mean "transform not only the components of the tensor $g$, but also the variable on which it depends".

Ah, right. The LHS is a simple Taylor expansion, whereas the RHS is the product of expansions of 3 transformations. I got lost figuring out exactly what needed transforming :-) Thanks again.

I could still do with help understanding the flaw in:

[Book 2.49] $x^{\mu}=0+\left( \frac{\partial x^{\mu}}{\partial x^{\hat{\mu}}} \right)_{p}x^{\hat{\mu}}+\frac{1}{2}\left( \frac{\partial ^{2}}{\partial x^{\hat{\mu_{1}}}\partial x^{\hat{\mu_{2}}}}\right)_{p}x^{\hat{\mu_{1}}}x^{\hat{\mu_{2}}} + ...$

Applying $\frac{\partial }{\partial x^{\hat{\mu}}}$ to this $x^{\mu}$ (LHS) gives $\frac{\partial x^{\mu}}{\partial x^{\hat{\mu}}}$, equivalent to Schutz $\frac{\partial x^{\alpha}}{\partial x^{\mu'}}$

Applying to RHS gives $\left( \frac{\partial x^{\mu}}{\partial x^{\hat{\mu}}} \right)_{p}+\frac{1}{2}\left( \frac{\partial ^{2}x^{\mu}}{\partial x^{\hat{\mu_{1}}}\partial x^{\hat{\mu_{2}}}}\right)_{p}x^{\hat{\mu_{2}}} + ...$

which seems to disagree with the coefficients in Schutz 6.23 ?

 

[DrGreg]

Applying to RHS gives $\left( \frac{\partial x^{\mu}}{\partial x^{\hat{\mu}}} \right)_{p}+\frac{1}{2}\left( \frac{\partial ^{2}x^{\mu}}{\partial x^{\hat{\mu_{1}}}\partial x^{\hat{\mu_{2}}}}\right)_{p}x^{\hat{\mu_{2}}} + ...$

which seems to disagree with the coefficients in Schutz 6.23 ?

I think you need to think this through a bit more carefully. For a start$$

\frac{\partial}{\partial x^\hat{\mu}} \left( \left( \frac{\partial x^{\mu}}{\partial x^{\hat{\mu}}} \right)_{p}x^{\hat{\mu}} \right)

$$doesn't even make sense as the index $\hat\mu$ appears three times, disobeying the tensor index summation conventions. The indexes in the other terms don't balance either. Each index should appear either once in every term of the equation, or else {twice or never} in every term.

 

[chartery]

I think you need to think this through a bit more carefully. For a start$$

OK, my problem was thinking the partial derivative would only apply to the explicit $x^{\hat{\mu}}$, and lacking enough understanding of the multiple indices to assist! Thank you.

 

[chartery]

Apologies for my simplistic struggles, but:

Carroll (book) 2.50, left side is
$(g_{\hat{\mu}{\hat{\nu}}}=) \left( \hat g \right)_{p}+\left( \hat{\partial } \hat{g}\right)_{p}\hat{x}+\left( \hat{\partial}\hat{\partial}\hat{g} \right)_{p}\hat{x}\hat{x}+$
which I take to be an expansion of $g_{\hat{\mu}{\hat{\nu}}}\left( x^{\hat{\alpha}} \right)$ in terms of $x^{\hat{\alpha}}$, with no transformations.

Filling in the indices, I get
$g_{\hat{\mu}{\hat{\nu}}}=\left( g_{\hat{\mu}{\hat{\nu}}} \right)_{p}+\left( \frac{\partial }{\partial x^{\hat{\alpha}}} g_{\hat{\mu}{\hat{\nu}}}\right)_{p}x^{\hat{\alpha}}+\left( \frac{\partial ^{2}}{\partial x^{\hat{\alpha}}\partial x^{\hat{\beta}}}g_{\hat{\mu}{\hat{\nu}}}\right)_{p}x^{\hat{\alpha}}x^{\hat{\beta}}+$
but cannot see where the expected coefficient of 1/2 for the third term of a Taylor expansion has gone to.

 

[strangerep]

Carroll (book) 2.50, left side is
$(g_{\hat{\mu}{\hat{\nu}}}=) \left( \hat g \right)_{p}+\left( \hat{\partial } \hat{g}\right)_{p}\hat{x}+\left( \hat{\partial}\hat{\partial}\hat{g} \right)_{p}\hat{x}\hat{x}+$
which I take to be an expansion of $g_{\hat{\mu}{\hat{\nu}}}\left( x^{\hat{\alpha}} \right)$ in terms of $x^{\hat{\alpha}}$, with no transformations.

Filling in the indices, I get
$g_{\hat{\mu}{\hat{\nu}}}=\left( g_{\hat{\mu}{\hat{\nu}}} \right)_{p}+\left( \frac{\partial }{\partial x^{\hat{\alpha}}} g_{\hat{\mu}{\hat{\nu}}}\right)_{p}x^{\hat{\alpha}}+\left( \frac{\partial ^{2}}{\partial x^{\hat{\alpha}}\partial x^{\hat{\beta}}}g_{\hat{\mu}{\hat{\nu}}}\right)_{p}x^{\hat{\alpha}}x^{\hat{\beta}}+$
but cannot see where the expected coefficient of 1/2 for the third term of a Taylor expansion has gone to.

Hmm. Neither can I. The $\frac12$ is missing from the 2nd-order term on both sides of (2.50).

I think what's going on is this: Carroll only needs the number of terms at each order, but doesn't need the multiplicative factors. [Read the paragraph following (2.50) to see this.] If he restored the $\frac12$ on both sides it wouldn't change the argument in that paragraph.

Btw, I recommend that you (or any GR student) download a copy of Matthias Blau's notes on General Relativity. In particular, Blau's section 3.6 derives the existence of locally inertial coordinates by 3 different methods. His final method, called "numerology", seems roughly equivalent to Carroll's method, but Blau's first 2 methods are more explicit.

Blau's notes are at a more advanced level than Carroll's book, and they cover more ground. (Blau is now my primary go-to source when I want to check something in GR, or delve deeper into some aspect.)

HTH.

 

[chartery]

Hmm. Neither can I. The $\frac12$ is missing from the 2nd-order term on both sides of (2.50).

Blau's notes are at a more advanced level than Carroll's book, and they cover more ground. (Blau is now my primary go-to source when I want to check something in GR, or delve deeper into some aspect.)

HTH.

That's a relief! Thanks very much again.
I will try Blau, albeit concerned at 'advanced-ing' before I can even walk.