- #1
- 24,492
- 15,012
Greg Bernhardt submitted a new PF Insights post
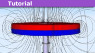
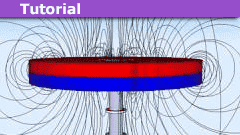
The Homopolar Generator: An Analytical Example
Continue reading the Original PF Insights Post.
The Homopolar Generator: An Analytical Example
Continue reading the Original PF Insights Post.