- #1
Trying2Learn
- 373
- 57
- TL;DR Summary
- When can you split the derivative?
Good Morning
I have read that it is not justified to split the "numerator" and "denominator" in the symbol for, say, dx/dt
However, when I look at Wikipedia's discussion on the Principle of Virtual Work, they do just that. (See picture, below).
I was told it is OK in 1D cases, but note the bold terms (vectors) and dot product: this is not assumed to be 1D
How do they get way with inserting a dt in the numerator (on the third term) and inserting a dt at the tail?
See picture, below...
Just to be clear: I do understand what is happening with the physics -- I am just confused with how they "almost whimisically" treat the derivative dr/dt as a quotient when I have read, many times, to see the derivative as ONE symbol, not as a ratio.
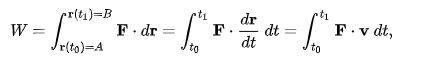
I have read that it is not justified to split the "numerator" and "denominator" in the symbol for, say, dx/dt
However, when I look at Wikipedia's discussion on the Principle of Virtual Work, they do just that. (See picture, below).
I was told it is OK in 1D cases, but note the bold terms (vectors) and dot product: this is not assumed to be 1D
How do they get way with inserting a dt in the numerator (on the third term) and inserting a dt at the tail?
See picture, below...
Just to be clear: I do understand what is happening with the physics -- I am just confused with how they "almost whimisically" treat the derivative dr/dt as a quotient when I have read, many times, to see the derivative as ONE symbol, not as a ratio.
Last edited: