Tree Diagram - Error at production

[mathmari]

Hey!

One box contains ten production parts, four of which have a production error.
Three parts are removed from the box one after the other without putting them back. We consider the following events :
A : the first production part that is removed is OK
B : the second production part that is removed is OK
C : the third production part that is removed is OK

Do we get the below diagramm?

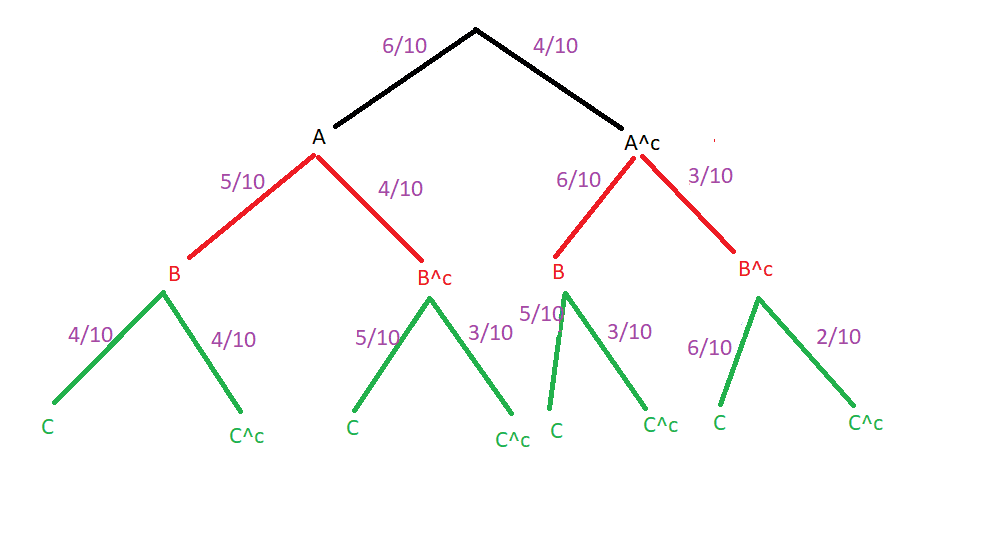
:unsure:

 

[I like Serena]

One box contains ten production parts, four of which have a production error.
Three parts are removed from the box one after the other without putting them back. We consider the following events :
A : the first production part that is removed is OK
B : the second production part that is removed is OK
C : the third production part that is removed is OK

Do we get the below diagram?

Hey mathmari!

After we pick a good item with probability $\frac 6{10}$, there are only 9 parts left in the box, aren't there?
Shouldn't the probability on another good item then be $\frac 59$ instead of $\frac 5{10}$? (Worried)

 

[mathmari]

After we pick a good item with probability $\frac 6{10}$, there are only 9 parts left in the box, aren't there?
Shouldn't the probability on another good item then be $\frac 59$ instead of $\frac 5{10}$? (Worried)

Ah yes! So should it be as follows?

:unsure:

 

[I like Serena]

Looks good to me. (Nod)

 

[mathmari]

Looks good to me. (Nod)

Do we have the following then ?
\begin{align*}&P(A)=\frac{6}{10} \\ &P(B\mid A)=\frac{5}{9} \\ &P(A^c\cap B^c)=P(B^c\mid A^c)\cdot P(A^c)=\frac{3}{9}\cdot \frac{4}{10}=\frac{2}{15} \\ &P(B)=P(B\cap A)+P(B\cap A^c)=P(B\mid A)\cdot P(A)+P(B\mid A^c)\cdot P(A^c)=\frac{5}{9}\cdot\frac{6}{10}+\frac{6}{9}\cdot \frac{4}{10} =\frac{1}{3}+\frac{4}{15}=\frac{3}{5}\\ &P(A\mid B)=\frac{P(A\cap B)}{P(B)} =\frac{P(B\mid A)\cdot P(A)}{P(B)}=\frac{\frac{5}{9}\cdot \frac{6}{10} }{\frac{3}{5}}=\frac{\frac{1}{3} }{\frac{3}{5}} =\frac{5}{9} \\ & P(A^c\cap B^c\cap C^c) =P(C^c\mid A^c\cap B^c)\cdot P(A^c\cap B^c)=P(C^c\mid A^c\cap B^c)\cdot \frac{2}{15} =\ \ ? \\ & P(A\cup B\cup C) = \ \ ? \\ & P(C\mid A\cap B^c) = \ \ ?\end{align*}

Could you give me a hint for the last three ones? :unsure:

 

[I like Serena]

Let's consider $P(C^c\mid A^c\cap B^c)$.
It reads as: given that the first part was bad and given that the second part was also bad, what is the chance that the third part is bad?
How many parts are left in the box, and how many of them are bad?
We can also see it in your tree diagram.

According to the general sum rule we have $P(A\cup B)=P(A)+P(B)-P(A\cap B)$.

Perhaps we can do $P(C\mid A\cap B^c)$ in the same way as $P(C^c\mid A^c\cap B^c)$.

 

[mathmari]

Let's consider $P(C^c\mid A^c\cap B^c)$.
It reads as: given that the first part was bad and given that the second part was also bad, what is the chance that the third part is bad?
How many parts are left in the box, and how many of them are bad?
We can also see it in your tree diagram.

Is it $\frac{2}{8}$ ? :unsure:

Can we calculate that also without using the tree diagram? :unsure:

According to the general sum rule we have $P(A\cup B)=P(A)+P(B)-P(A\cap B)$.

\begin{align*}P(A\cup B\cup C) &= P(A\cup B)+P(C)-P(A\cap B\cap C)\\ & =P(A\cup B)+P(C)-P(A\cap B\cap C)\\ & =P(A)+P(B)-P(A\cap B)+P(C)-P(A\cap B\cap C)\\ & =P(A)+P(B)-P(A\mid B)\cdot P(B)+P(C)-P(A\cap B\cap C)\end{align*} Every term is known, without the last one, right? How can we calculate this one? :unsure:

 

[I like Serena]

Is it $\frac{2}{8}$ ?

Can we calculate that also without using the tree diagram?

Yep. (Nod)

After taking 2 bad parts (given $A^c\cap B^c$), there are 2 bad parts left on a total of 8 parts. So we get $\frac 2 8$.
Isn't that how we constructed the tree diagram, and also how we found $P(A)$, $P(B\mid A)$, and so on?

\begin{align*}P(A\cup B\cup C) &= P(A\cup B)+P(C)-P(A\cap B\cap C)\\ & =P(A\cup B)+P(C)-P(A\cap B\cap C)\\ & =P(A)+P(B)-P(A\cap B)+P(C)-P(A\cap B\cap C)\\ & =P(A)+P(B)-P(A\mid B)\cdot P(B)+P(C)-P(A\cap B\cap C)\end{align*} Every term is known, without the last one, right? How can we calculate this one?

I'm afraid that is not correct. (Shake)

Instead we should have $P(A\cup B\cup C) = P(A\cup B)+P(C)-P((A\cup B)\cap C)$. (Sweating)

$P(A\cap B\cap C)$ is the chance that we get 3 parts that are OK in a row. Isn't that $\frac 6{10}\cdot\frac 5{9}\cdot \frac 4{8}$?

 

[mathmari]

So do we have the following ? \begin{align*}P(A\cup B\cup C) &= P(A\cup B)+P(C)-P((A\cup B)\cap C)\\ & =P(A\cup B)+P(C)-P((A\cap C)\cup (B\cap C))\\ & =P(A)+P(B)-P(A\cap B)+P(C)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C)\\ & =P(A)+P(B)-P(A\mid B)\cdot P(B)+P(C)-P(C\mid A)\cdot P(A)-P(C\mid B)\cdot P(B)+P(A\cap B\cap C)\\ & =\frac{6}{10}+\frac{3}{5}-\frac{5}{9}\cdot \frac{3}{5}+\left (\frac{6}{10}\cdot \frac{5}{9}\cdot \frac{4}{8}+\frac{6}{10}\cdot \frac{4}{9}\cdot \frac{4}{8}+\frac{4}{10}\cdot \frac{6}{9}\cdot \frac{5}{8}+\frac{4}{10}\cdot \frac{3}{9}\cdot \frac{6}{8}\right )-P(C\mid A)\cdot \frac{6}{10}-P(C\mid B)\cdot \frac{3}{5}+\frac{6}{10}\cdot \frac{5}{9}\cdot \frac{4}{8}\end{align*}
Is everything correct so far? :unsure:

Does it hold that $P(C\mid A)=\frac{5}{9}\cdot \frac{4}{8}+\frac{4}{9}\cdot \frac{5}{8}$ and $P(C\mid B) = \frac{4}{8}+\frac{5}{8}$ ? (The second one is wrong since it is greater than $1$.) ? :unsure:

 

[I like Serena]

So do we have the following ? \begin{align*}P(A\cup B\cup C) &= P(A\cup B)+P(C)-P((A\cup B)\cap C)\\ & =P(A\cup B)+P(C)-P((A\cap C)\cup (B\cap C))\\ & =P(A)+P(B)-P(A\cap B)+P(C)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C)\\ & =P(A)+P(B)-P(A\mid B)\cdot P(B)+P(C)-P(C\mid A)\cdot P(A)-P(C\mid B)\cdot P(B)+P(A\cap B\cap C)\\ & =\frac{6}{10}+\frac{3}{5}-\frac{5}{9}\cdot \frac{3}{5}+\left (\frac{6}{10}\cdot \frac{5}{9}\cdot \frac{4}{8}+\frac{6}{10}\cdot \frac{4}{9}\cdot \frac{4}{8}+\frac{4}{10}\cdot \frac{6}{9}\cdot \frac{5}{8}+\frac{4}{10}\cdot \frac{3}{9}\cdot \frac{6}{8}\right )-P(C\mid A)\cdot \frac{6}{10}-P(C\mid B)\cdot \frac{3}{5}+\frac{6}{10}\cdot \frac{5}{9}\cdot \frac{4}{8}\end{align*}
Is everything correct so far?

Yep. (Nod)

Does it hold that $P(C\mid A)=\frac{5}{9}\cdot \frac{4}{8}+\frac{4}{9}\cdot \frac{5}{8}$ and $P(C\mid B) = \frac{4}{8}+\frac{5}{8}$ ? (The second one is wrong since it is greater than $1$.) ?

How did you get them? (Wondering)
It looks as if $P(C\mid A)$ is correct, although I needed a couple of steps to get there.

As for the other one, don't we have:
$$P(C\mid B)=\frac{P(B\cap C)}{P(B)}=\frac{P((A\cap B\cap C)\cup (A^c\cap B\cap C))}{P(B)}
=\frac{P(A\cap B\cap C)+ P(A^c\cap B\cap C)}{P(B)}$$

 

[mathmari]

Ahh ok!

So do we have the following ?
\begin{align*}&P(A)=\frac{6}{10} \\ &P(B)=\frac{3}{5} \\ &P(A\mid B)=\frac{5}{9} \\ &P(A\cap B\cap C) = \text{Wkt dass wir 3 Teile nacheinander nehmen die in Ordnung sind}=\frac 6{10}\cdot\frac 5{9}\cdot \frac 4{8}=\frac 1{6}
\\ & P(C)=P(C\cap B\cap A)+P(C\cap B^c\cap A)+P(C\cap B\cap A^c)+P(C\cap B^c\cap A^c)\\ & =\frac{6}{10}\cdot \frac{5}{9}\cdot \frac{4}{8}+\frac{6}{10}\cdot \frac{4}{9}\cdot \frac{4}{8}+\frac{4}{10}\cdot \frac{6}{9}\cdot \frac{5}{8}+\frac{4}{10}\cdot \frac{3}{9}\cdot \frac{6}{8} = \frac{1}{6}+ \frac{2}{15}+\frac{1}{6}+\frac{1}{10}=\frac{17}{30} \\ &P(C\mid A) =\frac{P(A\cap C)}{P(A)}=\frac{P((A\cap B\cap C)\cup (A\cap B^c\cap C))}{P(A)}
=\frac{P(A\cap B\cap C)+ P(A\cap B^c\cap C)}{P(A)}\\ & =\frac{\frac{1}{6}+ \frac{2}{15}}{\frac{6}{10}} =\frac{\frac{3}{10}}{\frac{6}{10}}=\frac{1}{2} \\ &P(C\mid B)=\frac{P(B\cap C)}{P(B)}=\frac{P((A\cap B\cap C)\cup (A^c\cap B\cap C))}{P(B)}
=\frac{P(A\cap B\cap C)+ P(A^c\cap B\cap C)}{P(B)} \\ & =\frac{\frac{1}{6}+ \frac{1}{6}}{\frac{3}{5}} =\frac{\frac{2}{6}}{\frac{3}{5}}=\frac{\frac{1}{3}}{\frac{3}{5}}=\frac{5}{9} \end{align*}
:unsure:

 

[I like Serena]

Looks good to me! (Nod)

 

[mathmari]

Perhaps we can do $P(C\mid A\cap B^c)$ in the same way as $P(C^c\mid A^c\cap B^c)$.

The term $P(C\mid A\cap B^c)$ means: given that the first part was good and given that the second part was bad, what is the chance that the third part is good?
After taking $2$ parts,one goodand one bad, (given $A\cap B^c$), there are $5$ good parts left on a total of $8$ parts. So we get $\frac 5 8$, i.e. $P(C\mid A\cap B^c)=\frac 5 8$.

Is that correct? :unsure:

 

[I like Serena]

The term $P(C\mid A\cap B^c)$ means: given that the first part was good and given that the second part was bad, what is the chance that the third part is good?
After taking $2$ parts,one goodand one bad, (given $A\cap B^c$), there are $5$ good parts left on a total of $8$ parts. So we get $\frac 5 8$, i.e. $P(C\mid A\cap B^c)=\frac 5 8$.

Is that correct?

Yep. (Nod)

 

[mathmari]

Yep. (Nod)

Great!

We could calculate that also using the formula, right?
\begin{align*}P(C\mid A\cap B^c)=\frac{P(A\cap B^c\cap C)}{P(A\cap B^c)}=\frac{\frac{2}{15}}{P(B^c\mid A)\cdot P(A)}=\frac{\frac{2}{15}}{\frac{4}{9}\cdot \frac{6}{10}}=\frac{\frac{2}{15}}{ \frac{4}{15}}=\frac{2}{ 4}\end{align*}
I get a different result as previously... So can we not do that in that way? :unsure:

 

[I like Serena]

We could calculate that also using the formula, right?
\begin{align*}P(C\mid A\cap B^c)=\frac{P(A\cap B^c\cap C)}{P(A\cap B^c)}=\frac{\frac{2}{15}}{P(B^c\mid A)\cdot P(A)}=\frac{\frac{2}{15}}{\frac{4}{9}\cdot \frac{6}{10}}=\frac{\frac{2}{15}}{ \frac{4}{15}}=\frac{2}{ 4}\end{align*}
I get a different result as previously... So can we not do that in that way?

Don't we have that $P(A\cap B^c\cap C)=\frac 6{10}\cdot\frac 49\cdot \frac 58=\frac 16$ instead of $\frac 2{15}$?

 

[mathmari]

Don't we have that $P(A\cap B^c\cap C)=\frac 6{10}\cdot\frac 49\cdot \frac 58=\frac 16$ instead of $\frac 2{15}$?

Ah yes, I had a typo above! (Tmi)

I want to check now if the events $B$ and $A^c$ are independent, once by calculating and once by the tree diagram.

By calculating we have :

We have that $P(A^c\cap B)=P(B\mid A^c)\cdot P(A^c)=\frac{6}{9}\cdot \frac{4}{10}= \frac{4}{15}$ and $P(A^c)\cdot P(B)=\frac{4}{10}\cdot \frac{3}{5}=\frac{12}{50}$, sowe have that $P(A^c\cap B)\neq P(A^c)\cdot P(B)$, which means that the events $A^c$ and $B$ are not independent.

Is that correct? :unsure: How can we check that at the tree diagram? :unsure:

 

[I like Serena]

I want to check now if the events $B$ and $A^c$ are independent, once by calculating and once by the tree diagram.

By calculating we have :
We have that $P(A^c\cap B)=P(B\mid A^c)\cdot P(A^c)=\frac{6}{9}\cdot \frac{4}{10}= \frac{4}{15}$ and $P(A^c)\cdot P(B)=\frac{4}{10}\cdot \frac{3}{5}=\frac{12}{50}$, sowe have that $P(A^c\cap B)\neq P(A^c)\cdot P(B)$, which means that the events $A^c$ and $B$ are not independent.

Looks correct. (Nod)

How can we check that at the tree diagram?

We have 2 branches that correspond to $B$. One with $\frac 59$ and one with $\frac 69$.
Which branch we should have depends on $A$ and they do not have the same probability.
Therefore $B$ depends on $A$, which implies it also depends on $A^c$.

We can also express it as $P(B\mid A)=\frac 59\ne \frac 69=P(B\mid A^c)$, which shows that the probability on $B$ depends on $A^c$ and they are therefore not independent.