- #1
opus
Gold Member
- 717
- 131
Homework Statement
Back with more trig identities.
Verify that the following is an identity
##-tan\frac{a}{2} = cot\left(a\right)-csc\left(a\right)##
Homework Equations
All pythagorean identities, double angle formulas, half angle formulas
The Attempt at a Solution
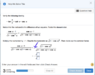
In the picture that I've attached, I am confused about where I annotated with the blue arrow. If I have ##cos\left(a\right)-1## and multiply by -1, I get ##1-cos\left(a\right)##. Then I'm told by the example to square root and square this expression. However, it still keeps a negative out in front of the fraction. So how can I multiply by -1, to change the expression, and also keep a negative out front of the fraction that wasn't there before? Shouldn't it be one or the other?