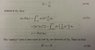- #1
Mary
- 11
- 0
I'm currently reading the book Introductory Quantum Mechanics by Richard Liboff 4th edition.
I'm reading one of the proofs and I don't understand what is happening in one of the steps.
The problem is trying to find the Hermitian adjoint of the operator [itex]\hat{D}[/itex]=[itex]\partial[/itex]/[itex]\partial[/itex]x defined in hilbert space
I have attached an image of the problem to this forum. The step I don't understand is circled. I understand where the last part (the - integral) comes in but the first part I do not understand. All I know is that it is equal to 0 and I don't know why. Thanks for any input.
I know this is probably just a simple math step I have probably forgotten about.
I'm reading one of the proofs and I don't understand what is happening in one of the steps.
The problem is trying to find the Hermitian adjoint of the operator [itex]\hat{D}[/itex]=[itex]\partial[/itex]/[itex]\partial[/itex]x defined in hilbert space
I have attached an image of the problem to this forum. The step I don't understand is circled. I understand where the last part (the - integral) comes in but the first part I do not understand. All I know is that it is equal to 0 and I don't know why. Thanks for any input.
I know this is probably just a simple math step I have probably forgotten about.