- #1
Kushwoho44
- 25
- 1
I have been trying to fully grasp the concept of the Cauchy stress tensor and so I thought I'd make a post where I clear up my confusion. There may be subsequent replies as I pose more questions.
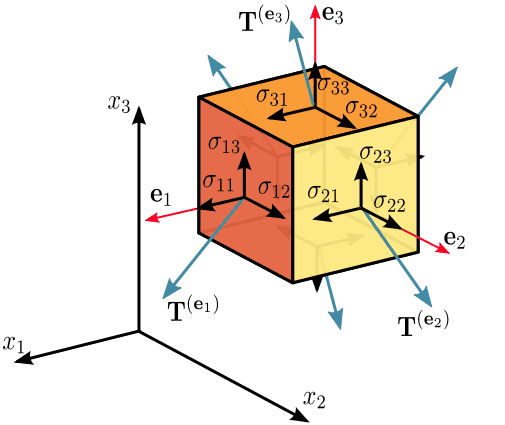
I am specifically confused at how the stress tensor relates to the control volume in the image above. My understanding has evolved to the conclusion: The stress tensor is defined at every point in the field, thus there would be a tensor defined at each point in the above control volume.
Questions: The control volume illustration above, though, seems to suggest that you can shrink the control volume to an infinitesimal element to where the stresses on that element will be described by the stress tensor. This is fine, but I cannot seem to understand how the stresses on the 'hidden' faces are included in the tensor? In the case of a fluid flowing, we cannot assume static condition and deduce that they are necessarily equal and opposite to the stresses on the 'front' faces?
Kind regards.
I am specifically confused at how the stress tensor relates to the control volume in the image above. My understanding has evolved to the conclusion: The stress tensor is defined at every point in the field, thus there would be a tensor defined at each point in the above control volume.
Questions: The control volume illustration above, though, seems to suggest that you can shrink the control volume to an infinitesimal element to where the stresses on that element will be described by the stress tensor. This is fine, but I cannot seem to understand how the stresses on the 'hidden' faces are included in the tensor? In the case of a fluid flowing, we cannot assume static condition and deduce that they are necessarily equal and opposite to the stresses on the 'front' faces?
Kind regards.