Understanding the Purpose of Charts in Differential Geometry

[Fgard]

I am studying differential geometry and I stumbled on something that I don't understand. When we have a m- dim differential manifold, with U_i and U_j open subsets of M with their corresponding coordinate

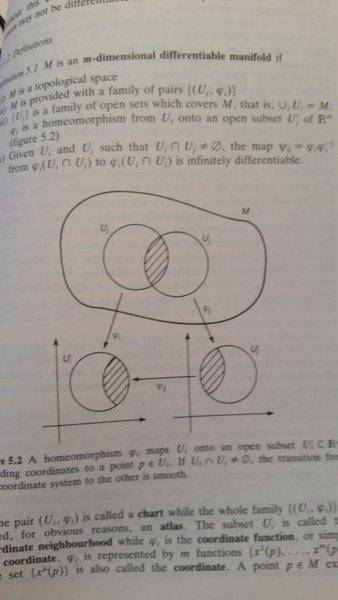
function phi. As can be seen in the figure.

If I understand it correctly phi_j of a point gives us a coordinate of that point. So what does the inverse of a coordinate function do? And how come the product of phi_i * phi_j = psi takes us between subsets?

 

[fresh_42]

The idea behind is that charts are a locally Euclidean map (coordinates) of the (curved) manifold. Just as street maps in an atlas are. Earth isn't flat, but locally we can pretend it is. This concept requires that overlapping charts are identical on their intersection.
The image in the textbook says $φ_i|_{U_i ∩ U_j} = Ψ_i \cdot φ_j|_{U_i ∩ U_j}$.

 

[Erland]

It is $\phi_i\phi_j^{-1}$ which maps a subset of $U'_j$ to a subset of $U'_i$, as is written on the page you scanned near the right margin on the upper half.

 

[Fgard]

So that [tex]$\Psi$[\tex] maps between different subsets comes from a definition?

 

[Samy_A]

So that [tex]$\Psi$[\tex] maps between different subsets comes from a definition?

Yes.
Set $U_{ij}=U_i \cap U_j$, and assume that $U_{ij}\neq \varnothing$
$\Psi_{ij}$ by definition maps $\phi_j(U_{ij})$ to $\phi_i(U_{ij})$.
$\Psi_{ij}$ being infinitely differentiable is the condition imposed in (iv) for M to be an m-dimensional differentiable manifold.

As said above you can view $\Psi_{ij}$ as a coordinate transformation. Point (iv) in the definition requires these transformations to be infinitely differentiable.

The book explains it better than I could, actually:

 

[Fgard]

Okej. Thank you very much for all the help.

 

[lavinia]

If I understand it correctly phi_j of a point gives us a coordinate of that point. So what does the inverse of a coordinate function do? And how come the product of phi_i * phi_j = psi takes us between subsets?

The inverse of a coordinate chart is called a "parameterization". It assigns points on the manifold to parameters in a domain in Euclidean space.

Example:

$φ(u,v) = (sin(u)cos(v),sin(u)sin(v),cos(u))$ parameterizes a region of the sphere. (u and v need to be restricted so that the map is 1 to 1).

Another Example:

$φ(u,v) = (cos(u),sin(u),cos(v),sin(v))$ parameterizes a torus in four dimensional Euclidean space.

A parameterization generalizes the idea of a parameterized curve,$c(t)$, to more than one parameter.

- A coordinate chart goes in the other direction. It assigns a domain in Euclidean space to points on a manifold.

Example: Project the northern hemisphere (minus the equator) of the unit sphere onto the open unit disk in the xy-plane by dropping the z-coordinate.

- A parameterization followed by a coordinate chart maps a domain in Euclidean space into another domain in Euclidean space. If $ψ$ and $φ$ are two coordinate charts then $φψ^{-1}$ is a parameterization followed by a coordinate chart.

For smooth manifolds,$φψ^{-1}$ is required to be a smooth map.

 

[zinq]

Here's a bit of intuition about charts. An n-manifold M is a space that is locally like Euclidean space of dimension n. If M is a smooth n-manifold — the nicest kind — then it makes sense to talk about smooth functions

f: M → ℝ​

on it, smooth curves

α: [a,b] → M​

on it, smooth vector fields

V: M → T(M)​

on it, etc. (Here T(M) is the tangent space of M, a concept that your course will soon introduce, which consists of all tangent vectors at all points of M.)

In order to achieve this, we can always construct M by taking pieces (open sets) of Euclidean space ℝⁿ and "gluing them together smoothly". The idea of charts with their smooth transition functions is the right way to make this idea of smooth glueing precise, and allows for definition of smooth functions, curves, vector fields, etc. associated with M.