Variation sign and integral sign

[thaiqi]

TL;DR Summary

wondering about a proof of exchange between variation sign and integral sign

Hello, everyone.
I know that it is feasible to exchange the order of one variation sign and one integral sign. But there gives a proof of this in one book. I wonder about a step in it. As below marked in the red
rectangle:

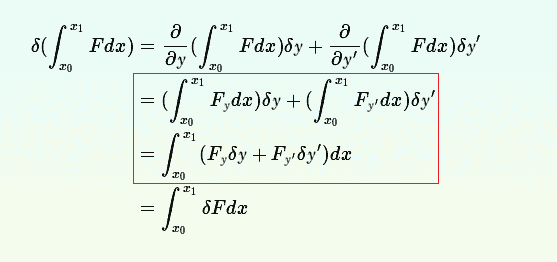
How can $\delta y$ and $\delta y^\prime$ be moved into the integral sign? Aren't they functions of $x$ ?

 

[jambaugh]

You are correct in that the $\delta y$ and $\delta y'$ should not, as shown, appear outside the integrals. There is a bit of slopyness in the notation we use where we utilize the same names for variables and the functions such as $y_{variable}= y_{function}(x)$. I'll walk through the above derivation in this context in a moment to show you what I mean.

Now you have not given the context of this derivation but I will make some assumptions and you can correct me if I err. Below I will distinguish functions from variables by using greek. I.e. if $x,y$ are respectively independent and dependent variables, that dependency is given by a function, say $y = \varphi(x)$. (Toward the end I'll revert back to y as function.)

It looks to me like you are taking the variation of a functional, let's call it $S$ defined by:

$$S[\phi] = \int_{x_1}^{x_2} F(x,\phi(x),\phi'(x)) dx$$
by analogy compare this to some scalar valued function of a vector $\sigma(\mathbf{v})$. (Note that here I use brackets [] to indicate a (not necessarily linear) operator's action on a function as a whole. Rather than a function action on its value as a composition of functions.)

The variation $\delta S$ is analogous to the differential of the scalar valued function but since we don't have a nice indexible expansion it is harder to express in terms of components. It however has a given form in contrast to my arbitrary vector function analog. So let's break it down in terms of functional derivatives and limits of difference quotients:
$\delta S[\varphi]$ is the value of a linear functional on the variation of $\varphi$ defined by the Gateaux differential and derivative:
$$\delta S[\varphi] = S'[\varphi][\delta\varphi]= \lim_{h \to 0} \frac{1}{h}\left(S[\varphi+h\delta\varphi]-S[\varphi]\right)$$
Here $\delta\varphi$ is an independent variation of the function in the same sense that say $d\mathbf{v}$ is an independent differential vector in the vector differential relation:
$$d\sigma(\mathbf{v})= \nabla\sigma(\mathbf{v})\bullet d\mathbf{v}$$
In this vector example the linear functional can, via the Riesz Representation Theorem be expressed by dotting with a vector. The gradient is the dual of the vector derivative of $\sigma$.

So taking the form of $S$ and applying the limit of the difference quotient we get:
$$\delta S[\varphi][\delta\varphi] = \lim_{h\to 0} \frac{1}{h}\left( \int_{x_0}^{x_1} F(x,\varphi(x)+h\delta\varphi(x), \varphi'(x)+h\delta\varphi'(x)) - F(x,\varphi(x),\varphi'(x))dx\right)$$
Remembering that the variation $\varphi$ is arbitrary and applying linearity to the integral we can internalize the limit of the difference quotient into the integral to yield an integral of partial derivatives:
$$\delta S=\int_{x_0}^{x_1} \left(F_2(x,\varphi(x),\varphi'(x)) \delta\varphi(x) + F_3(x,\varphi(x),\varphi'(x))\delta\varphi'(x) \right)dx = \int_{x_0}^{x_1} \delta F(x,\varphi(x),\varphi'(x))dx$$

That is the derivation properly denoted. However as you can see the explicit details can be a bit overwhelming so one typically invokes some (somewhat sloppy) shortcuts. That slightly erroneous first step works because one is invoking a "functional gradient" in a sense when treating "$\delta y$" as a differential vector (in the space of differentiable functions on the interval $I=[x_0,x_1]$).
$$\delta S = \frac{\delta}{\delta y}\left(\int_I F dx\right)[\delta y] = \nabla_y\left(\int_I F dx\right)\bullet \delta y$$
where this "dot product" would be an integral contraction with another variable of integration, say $\tilde{x}$. The fact that $\delta y$ as a functional differential is arbitrary doesn't quite imply that its value and derivative are independent. But one can invoke say arbitrary linear combinations of a delta function and the derivative of a delta function at separate points, e.g.
$\delta y(x) = p\delta(x-a)+q\delta'(x-b)$
to show that the "sloppy" method will still lead to a valid result. I finally understood these variational derivations much better when I explored the implications of using the Gateaux differential and derivative in functional analysis. It is a little bulkier but one can get to the result without "bastardizing" the notation.

One final point I'd make. Integration of a function on a fixed interval is a linear functional. Consider in general that the derivative of a vector mapping is a linear operator (the Jacobi matrix represents this operator for vector mappings which are coordinate transformations.) If you look at the generalized derivative of a linear operator it will in fact be its own derivative.
For scalars: $a: x \mapsto y=ax$ means $a(x)' = (ax)'=a$
For linear maps: $A: \mathbf{x}\mapsto \mathbf{y}=A\mathbf{x}$ means $\frac{d\mathbf y}{\mathbf{x}} = A$.
This makes more sense when we look at differentials (remembering derivatives are mappings of differentials to differentials)
$$y =ax\to dy = adx,\quad \mathbf{y}=A\cdot \mathbf{x}\to d\mathbf{y}=A\cdot \mathbf{x}$$
This applies to function mappings since they are, after all, just another form of vector mapping:
$I [\varphi] = \int_{[a,b]}\varphi(t) dt$ is linear and so $\delta (I[\varphi] = I\cdot\delta \varphi$.

This is, I think the gist of what your author is deriving for the case at hand IMNSHO.

 

[thaiqi]

You are correct in that the $\delta y$ and $\delta y'$ should not, as shown, appear outside the integrals. ……

First thanks very much for your reply. I don't understand very well all parts of what you said. Do you agree it is a wrong step in the rectangle marked step at the third equal sign(though the result happens to be valid)? (Besides, I didn't say $\delta y$ and $\delta y'$ should not appear outside the integrals, but I said they cannot be moved into the integral. )

 

[jambaugh]

To answer your direct question, it is really a matter of the reverse, moving the $\delta y, \delta y'$ outside the integral from the inside which would be a mistake. In point of fact, it's the very first step that has questionable validity.

Again it is a question of conflating the meaning of $y$, at one level as a variable with respect to which one can take a partial derivative when it appears inside a function an at another level as a function of $x$ which may occur within a definite integral.

As an exercise try evaluating each step in this derivation sequence for specific examples. Say let $F(x,y,y')=x^2\cdot y^2\cdot y'$ and let $x_0 = 0, x_1=1$. For the initial functional and then the first derivation step one must evaluate the definite integral before considering variations or partial derivatives. To integrate you can't leave $y$ and $y'$ independent variables. They must be assigned some functional dependency on $x$. Let's choose one, say $y=x^3, y'=3x^2$. Then when you evaluate the definite integral you get a constant value. What does it mean to take the partial derivative of that with respect to $y$ or $y'$.

Alternatively if you treat $y$ and $y'$ as independent variables, then the integration would be:
$$\int_0^1 F(x,y,y')dx = \int_0^1 x^2 y^2 y' dx = \left[\frac{x^3}{3}\right]^1_0 y^2 y' = \frac{1}{3}y^2 y'$$
That is most definitely not what is intended here.

Phrased properly the partial derivatives of the first step should be a single functional derivative of the integral as a functional on $y$
$$= \frac{\delta }{\delta y}\left(\int_I F(x,y(x),y'(x))dx\right)[\delta y] = *...$$
The functional derivative should yield a (linear) functional acting on the variation of $y$ the function.

But you can then, for the purposes of expanding in terms of partial derivatives, consider $y$ and $y'$ independent functions of $x$ (and here I'm going to go greek to emphasize these functions) and expand this in terms of partial functional derivatives:
$$*=\left. \frac{\delta}{\delta \phi}\left(\int_I F(x,\phi(x),\psi(x))dx\right)\right\rvert_{(\phi,\psi)=(y,y')}[\delta y] ...$$
$$+\frac{\delta}{\delta \psi}\left(\int_I F(x,\phi(x),\psi(x))dx\right)\rvert_{(\phi,\psi)=(y,y')}[\delta y']$$
The next step would then be to internalize the partial functional derivative which would then manifest as an integral of standard partial derivatives of the integrand function F.

It's bulky to express this correctly. What is happening is that each "partial functional derivative" of a functional is yielding a linear functional valued functional which is evaluated at a functional differential. e.g.
$$A[y]= \int_a^b F(x,y(x))dx,\quad \frac{\delta}{\delta y}A[y]=B[y], \quad (B[y])[z]=\int_a^b F_2(x,y(x))\cdot z(x) dx$$
Here $x$ is a variable, and $y,z$ are functions (function valued variables to be precise). Also btw $F_2(u,v)=\frac{\partial}{\partial v}F(u,v)$. I'm here again using [] to indicate evaluation of a functional in analogy to but distinguished from standard function notation's ().

 

[thaiqi]

To answer your direct question, it is really a matter of the reverse, moving the $\delta y, \delta y'$ outside the integral from the inside which would be a mistake. In point of fact, it's the very first step that has questionable validity.
...

Thanks very much for your guidance again.