Volume of revolution -- Why use this integral?

[opus]

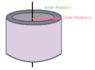
My question is, why is the circled integral the chosen integral for this case?
My thoughts are that we don't just use $\int_0^1e^{-x}$ because we need to make this two dimensional area into a three dimensional volume by doing 360 degrees of rotation. This would correspond to $2πr$. $2π$ is a constant and can be brought out front so I see why the $2π$ is there.
My question is, the radius is just 1, so why is there an $x$ in the integrand?

 

[phyzguy]

The radius of the shells is not 1. You're calculating the brown volume in your diagram by adding up the blue shells. Look at the blue shell. It is a cylindrical shell with height $e^{-x}$, width dx, and radius x. So its volume is $2 \pi x e^{-x} dx$.

 

[opus]

Ok I'm almost there. So by shell, we're talking about the hockey puck shaped thing. What's the rectangle representing and why is the width dx? I understand what it means for a simple area under curve, but the rotation is throwing me off. I can see the height and radius reasoning.

 

[opus]

Let me see if I can clean my question up.
If I look at this in terms of stacking the "hockey pucks" on top of each other, the height of each puck would be $e^{-x}$ and the radius would be $x$. Then I multiply by 2π to get the full rotation. With this picture in my mind, the $dx$ is confusing me. To stack the pucks on top of each other, the heights would have to get smaller and smaller. In other words, $dy$. But then looking at it this way, it would do be the height which is supposed to be $e^{-x}$

 

[phyzguy]

Ok I'm almost there. So by shell, we're talking about the hockey puck shaped thing. What's the rectangle representing and why is the width dx? I understand what it means for a simple area under curve, but the rotation is throwing me off. I can see the height and radius reasoning.

No, it's not a "hockey-puck shaped thing". When doing these volume integrals, that shape is usually called a "washer". The cylindrical shells you are integrating here are shaped like the wall of a soda can (without a top and bottom). See the attached sketches for "shells" vs "washers". You can do these problems either way as long as you are consistent. Try setting up your problem both ways and see if you get the same answer.

"washers":

"shells":

 

[opus]

Thanks for the visuals. The top one makes sense to me. The shell method, not at all. The shell just looks like the washer but with a hole punched through it, so how can it account for the volume if it's hollow?

 

[phyzguy]

It has a volume. It is $\pi (r2^2 - r1^2) h$. If the shell is thin, you can take the limit of the thickness dr = r2-r1 going to zero. Then the volume becomes $2 \pi h r dr$. You then build up a large number of concentric shells, like in the attached drawing:

 

[Mark44]

The shell just looks like the washer but with a hole punched through it

A washer has a hole punched through it.

 

[opus]

Ohhh ok. Thanks guys. I just had to let me brain stop thinking about it for a bit and then come back to it. So used to just thinking about 2 dimensional rectangles that I was having a hard time thinking 3 dimensionally like that.

 

[phyzguy]

Ohhh ok. Thanks guys. I just had to let me brain stop thinking about it for a bit and then come back to it. So used to just thinking about 2 dimensional rectangles that I was having a hard time thinking 3 dimensionally like that.

if you think you get it now, I strongly suggest doing your volume calculation with both methods (shells and washers) and make sure you get the same answer. This will test if you really understand.

 

[opus]

if you think you get it now, I strongly suggest doing your volume calculation with both methods (shells and washers) and make sure you get the same answer. This will test if you really understand.

I 100% agree. I tried this and didn't quite get the result that I had hoped, so I'm poking at it and watching some videos because I think I understand it, but can't explain it satisfactorily. Not really sure what question to ask so I'm doing some prodding to see if it comes to me how I'd like it to. I think I need to do a full start to finish on this thing because the text just glazed over it for an example to show how to integrate by parts, so I don't think it's intention was exactly to teach about shells and stuff. But now that I've started it, I want to understand how to do them.

 

[Mark44]

Something that is very helpful with either method is to make two drawings -- the first drawing is the region in the plane that will be revolved. The second drawing is a three-D drawing of a typical washer or shell. @phyzguy's first drawing in post #5 is an example of what I'm talking about. It's very important to get a good visual idea of what you are doing. This is much more important than just memorizing some formulas.

 

[opus]

Thanks Mark. Is there any kind of graphical software that can supplement this?

 

[Mark44]

Thanks Mark. Is there any kind of graphical software that can supplement this?

There probably is, but I don't use any software for these kinds of problems. To me it's just as quick to draw a couple of sketches and set up my integral based on them.