What is the area of rectangle ABCD?

[Albert1]

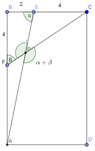
$Rectangle\,\,ABCD\,\,given\,\, point \,\,E,F \,\,on \,\,\overline {BC},\overline {AB}\,\,\, respectively$
$if \,\,\overline{BF}=\overline{CE}=4,\overline{BE}=2,point \,\, P \,\,is\,\, the \,\, intersection\,\ of\,\,\overline{AE}\,\,and\,\,\overline{CF},\,\, and \,\, \angle APC=\angle AEB+\angle CFB$
$please\,\,find \,\, the \,\, area \,\, of \,\, rectangle \,\,ABCD$

 

[lfdahl]

My attempt:

Spoiler

View attachment 6288
Let
\[\alpha =\angle AEB\: \: \: and \: \: \: \beta =\angle CFB\]

Note, that

\[\angle APC = \angle FPE = \alpha +\beta\]

The quadrilateral, $BFPE$, has the angle sum:

\[90^{\circ}+2( \alpha +\beta )=360^{\circ}\]

Thus, $\alpha + \beta = 135^{\circ}$

$\alpha$ and $\beta$ are easily calculated:

\[\tan\beta =\frac{\overline{BC}}{\overline{BF}}=\frac{3}{2}\Rightarrow \: \: \beta =56,31^{\circ}\]

\[\alpha = 135^{\circ}-56,31^{\circ}=78,69^{\circ}\]

Finally, $FA$ is found:

\[\tan \alpha =\frac{4+\overline{FA}}{2}\Rightarrow \overline{FA}=6.\]

Thus, the rectangle, $ABCD$, has the area: $6 \cdot 10 = 60$.

 

[Albert1]

My attempt:

Spoiler

Let
\[\alpha =\angle AEB\: \: \: and \: \: \: \beta =\angle CFB\]

Note, that

\[\angle APC = \angle FPE = \alpha +\beta\]

The quadrilateral, $BFPE$, has the angle sum:

\[90^{\circ}+2( \alpha +\beta )=360^{\circ}\]

Thus, $\alpha + \beta = 135^{\circ}$

$\alpha$ and $\beta$ are easily calculated:

\[\tan\beta =\frac{\overline{BC}}{\overline{BF}}=\frac{3}{2}\Rightarrow \: \: \beta =56,31^{\circ}\]

\[\alpha = 135^{\circ}-56,31^{\circ}=78,69^{\circ}\]

Finally, $FA$ is found:

\[\tan \alpha =\frac{4+\overline{FA}}{2}\Rightarrow \overline{FA}=6.\]

Thus, the rectangle, $ABCD$, has the area: $6 \cdot 10 = 60$.

Spoiler

Your answer is correct,thanks a lot .
But how do you get the value of $tan\,\alpha$ using a calculator ? if so try not

 

[Greg]

Here it is without aforementioned device (if such a device was actually used).

Spoiler

Using lfdahl's diagram and the result $\alpha+\beta=135^\circ$,

$$\tan(\alpha+\beta)=-1=\frac{\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\tan(\beta)}=\frac{\tan(\alpha) + 3/2}{1-3\tan(\alpha)/2}\implies\tan(\alpha)=5$$

and the result follows.

 

[lfdahl]

Spoiler

Your answer is correct,thanks a lot .
But how do you get the value of $tan\,\alpha$ using a calculator ? if so try not

Spoiler

Without the use of a calculator:
\[\tan(\beta )=\frac{3}{2} \\\\ \tan(\alpha +\beta )= \tan(135^{\circ})=\tan(90^{\circ}+45^{\circ})=-1 \\\\ \tan(\alpha +\beta )=\frac{\tan(\alpha )+\tan(\beta )}{1-\tan(\alpha )\tan(\beta )}\Rightarrow \tan(\alpha )=5 \\\\ \tan(\alpha )=\frac{\overline{AB}}{2}\Rightarrow \overline{AB} = 10\]