- #1
Karol
- 1,380
- 22
Homework Statement
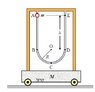
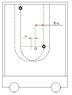
The bead of mass m starts to slide without friction from point A. the mass of the cart and the rail is M.
What is the max displacement of the wagon during the motion of the bead?
What is the force the rail exerts on the cart when the cart's velocity is maximum?
What is the impulse exerted on the bead from the moment it passes for the first time at point B until it passes the first time at point C?
Homework Equations
Impulse and momentum: Ft=mv
The Attempt at a Solution
Relative to the origin at the center of the arc, point O, the COM, at the beginning, is:
$$x_cm=\frac{-mR}{m+M}$$
The bead moves to the other side and the COM moves to a distance x from the origin:
$$\frac{-mR}{m+M}=\frac{mR-xM}{m+M}\Rightarrow x=\frac{2rm}{M}$$
The displacement of the wagon is:
$$\Delta x=\frac{2rm}{M}-\frac{mR}{m+M}$$
The force the rail exerts on the cart when the cart's velocity is at the max is zero since then the bead is at the lowest position (point C), it's velocity is horizontal and it doesn't exert any force on the rail.
The impulse from point B to C:
$$Ft=mv\rightarrow Ft=m(v_c-v_b)$$
Attachments
Last edited: