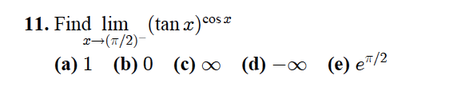What is the more appropriate method to solve for the limit in this scenario?

[Umar]

I've got another limit question here, but I don't suppose you use the same method as last time for sure (rational).

View attachment 6190

I essentially got (infinity)^0 and just assumed that to be equal to 1 which made sense to me. However, in my textbook and notes, (infinity) to the power of 0 is one type of an indeterminate form. Is there a more appropriate way to sovle this? Perhaps L'Hospital's Rule, although I tried it and get the answer to be 0 instead.

 

[MarkFL]

I would write:

$$L=\lim_{x\to\frac{\pi}{2}^{-}}\left(\left(\tan(x)\right)^{\cos(x)}\right)$$

Take the natural log of both sides, and apply log properties:

$$\ln(L)=\lim_{x\to\frac{\pi}{2}^{-}}\left(\cos(x)\ln\left(\tan(x)\right)\right)$$

This is indeed the indeterminate form $0\cdot\infty$, so let's transform it as follows:

$$\ln(L)=\lim_{x\to\frac{\pi}{2}^{-}}\left(\frac{\ln\left(\tan(x)\right)}{\sec(x)}\right)$$

Now, we have the indeterminate form $$\frac{\infty}{\infty}$$, and we may apply L'Hôpital's Rule:

$$\ln(L)=\lim_{x\to\frac{\pi}{2}^{-}}\left(\frac{\dfrac{\sec^2(x)}{\tan(x)}}{\sec(x)\tan(x)}\right)=\lim_{x\to\frac{\pi}{2}^{-}}\left(\frac{\cos(x)}{\sin^2(x)}\right)=\frac{0}{1^2}=0$$

Thus:

$$L=e^0=1$$