Why can't a particle ever reach a non-terminating decimal form radian value?

[Vinay080]

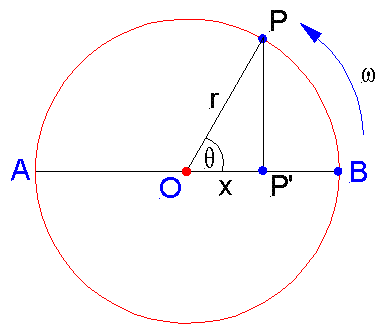
Consider a particle P moving in a circle of radius r as shown in the figure.
Premise 1: Position of the particle can be described by the angle θ.
Premise 2: Particle reaches the position with an angle θ if it has covered the angle lesser than θ.
Premise 3: Particle can never reach non-terminating decimal form radian value.
For example: 0.33333...rad; The particle can never reach this radian value because, to reach this value, first particle needs to cover 0.33 rad, then 0.333 rad, then 0.33333, and so on. Particle needs to go on and on, and the sequence of 0.333.. never ends.
Premise 4: As the particle can never reach non-terminating decimal form radian value, it can't even reach neighbor terminating decimal form radian value. For example 0.4 (considering 0.333.. of Premise 3) can never be reached as 0.333... can never be reached.

The argument, as evident, is in the zeno version. But, I am not able to come out of this cage. What is going wrong in this argument? Can the particle never reach non-terminating decimal form value? I think this problem can be generalized to all the physical quantities.

I had discussed a similar problem here: https://www.physicsforums.com/threads/diagonal-length-problem.806206/

 

[mfb]

Particle needs to go on and on, and the sequence of 0.333.. never ends.

And all those steps together can be done in finite time.
The resolution is exactly the same as for the linear case (you don't need the circle here at all). You can reach an infinite number of real numbers in a finite time.

 

[Vinay080]

Particle needs to go on and on, and the sequence of 0.333.. never ends.

And all those steps together can be done in finite time.
The resolution is exactly the same as for the linear case (you don't need the circle here at all). You can reach an infinite number of real numbers in a finite time.

Yes, I agree that, in reality it seems that particle completes the sequence 0.3, 0.33, 0.333, 0.333 and so on, in finite time.
But, the question is about whether particle completes the sequence (0.3, 0.33, 0.333, 0.333...) or not, based on the logic given, i.e 0.333... sequence has no end, so the particle can never complete this sequence, so the particle can never reach the subsequent terminating decimal form radian value. I see this problem as more on how to break this logical reasoning rather than getting satisfied by other reasons.

 

[mfb]

sequence has no end, so the particle can never complete this sequence

There is no reason why the second part should follow from the first one.

 

[Dale]

sequence has no end, so the particle can never complete this sequence,

Why not? What does it even mean for a particle to complete a sequence and why would a sequence being infinite prevent completion.

 

[Vinay080]

sequence has no end, so the particle can never complete this sequence,

There is no reason why the second part should follow from the first one.

Why not? What does it even mean for a particle to complete a sequence and why would a sequence being infinite prevent completion.

Sorry, I think, I was not clear in my thought.

Let me qutote the premise 3 (modified), which I posted first in the first post of this thread :

Premise 3: Particle can never reach non-terminating decimal form radian value.
For example: 0.33333...rad; The particle can never reach this radian value because, to reach this value, first particle needs to cover 0.33 rad, then 0.333 rad, then 0.33333, and so on. Particle needs to go on and on, and it can never reach 0.333... non-terminating value.

I will be happy if you can please redefine my faults (if there are any).

 

[sophiecentaur]

I will be happy if you can please redefine my faults (if there are any).

Perhaps it would help if you were to realize that each of the steps you are describing will take progressively less and less time to complete. The total time taken will be the sum of all those steps - which is finite! and that doesn't correspond to your "never".

 

[russ_watters]

Vinay080, Zeno's paradox was bad math and logic even when Zeno first proposed it. Your basic error is the same as Zeno's: (As sophiecentaur said) nowhere in anything you've written have you considered the time taken for each step. How can you possibly conclude anything about how long all steps will take unless you've considered how long each individual step takes?

 

[DrGreg]

Premise 3: Particle can never reach non-terminating decimal form radian value.
For example: 0.33333...rad; The particle can never reach this radian value because, to reach this value, first particle needs to cover 0.33 rad, then 0.333 rad, then 0.33333, and so on. Particle needs to go on and on, and it can never reach 0.333... non-terminating value.

By this logic, you would conclude that the sequence 0.3, 0.33, 0.333, 0.3333, 0.33333, ... diverges to a value of infinity. Do you really believe that? Don't you accept that it converges to ⅓?

 

[russ_watters]

By this logic, you would conclude that the sequence 0.3, 0.33, 0.333, 0.3333, 0.33333, ... diverges to a value of infinity. Do you really believe that? Don't you accept that it converges to ⅓?

No, typically, that's not how the [il]logic goes. Typically, it's just a matter of the implicit assumption that each step takes the same amount of time, therefore an infinite number of steps takes an infinite amount of time. That doesn't have anything to do with whether the value converges to 1, it's just a different formulation of an infinite sequence than Zeon used to illustrate the same thing (1/2+1/4+1/8...).

 

[jbriggs444]

No, typically, that's not how the [il]logic goes. Typically, it's just a matter of the implicit assumption that each step takes the same amount of time, therefore an infinite number of steps takes an infinite amount of time. That doesn't have anything to do with whether the value converges to 1, it's just a different formulation of an infinite sequence than Zeon used to illustrate the same thing (1/2+1/4+1/8...).

I think the implicit assumption is more like "any sequence of actions that can be completed must have a last action". The modern vision of infinite sequences makes that assumption false, of course.

 

[Dale]

The particle can never reach this radian value because, to reach this value, first particle needs to cover 0.33 rad, then 0.333 rad, then 0.33333, and so on.

OK, so what? What is it about "covering" a sequence of positions that you think prevents covering an infinite sequence of positions? You don't even need to go to a non-terminating decimal number like 1/3. You can just consider the infinite number of positions between 0.33 and 0.333. There already are an infinite number of positions there and you seem to accept that that infinite number of points could all be reached, so why not the remaining points between 0.333 and 1/3?

I am trying to help you spot your own error, but if this is just confusing you, then simply google for Zeno's paradox. This is all very standard stuff with lots of information about how it is resolved.

 

[Vinay080]

Thank you very much @jbriggs444. I meant exactly what you meant, if I have understood correctly what you meant. I look forward to understand the modern vision of infinite sequences which makes it false. If you have any suggestions on topics/books I should read, I will be privileged. But, @russ_watters "implicit assumption" was new to taste for me. Finally, a good point coming from @DaleSpam will sure help for my further understanding of this concept.

 

[jbriggs444]

Thank you very much @jbriggs444. I meant exactly what you meant, if I have understood correctly what you meant. I look forward to understand the modern vision of infinite sequences which makes it false. If you have any suggestions on topics/books I should read, I will be privileged. But, @russ_watters "implicit assumption" was new to taste for me.

Mathematics has a number of notions of "infinity". We are concerned with a specific sort here, the idea of an infinite set. That is, a set that has infinitely many members. Consider, for instance, the natural numbers as a set.

The first thing to remember is that the membership of a set is fixed. It does not change. We view the set of natural numbers is completed whole. It is not something that is a "potential infinity" which is as large as we need it to be for the task at hand. It is not a never ending process where we keep adding numbers to the set forever. The set of natural numbers is fixed and every natural number is a member.

That can be a hard concept to wrap your head around. It is key.

The natural numbers are characterized by the Peano Axioms (http://en.wikipedia.org/wiki/Peano_axioms). Those axioms make explicit that every natural number has a successor. There is no last natural number. There is nonetheless, a set containing all of them.