- #1
erogard
- 62
- 0
Hi everyone,
so let me introduce the scalar function [tex]\Phi[/tex] = -(x2+y2+z2)(-1/2) which some of you may recognize as minus one over the radial distance from the origin.
When I compute [tex]\nabla[/tex]2[tex]\Phi[/tex] is get 0.
Now if I do the following integral on the surface S of the unit sphere x2+y2+z2= 1 :
[tex]\int[/tex][tex]\int[/tex][tex]\nabla[/tex][tex]\Phi[/tex][tex]\bullet[/tex]n dS
I obtain 4[tex]\pi[/tex] which is just the surface area of the unit sphere since the laplacian of [tex]\Phi[/tex] dotted with the unit radial vector turns out to be one.
Yet the Divergence Theorem
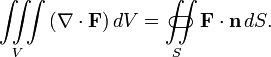
tells me precisely that those two quantities should be equal, but integrating the laplacian of phi would give me zero since the latter quantity is already 0.
Any idea on what I'm doing wrong?
(please only suggestion but do not give me the answer straight away if you think you know it, I'd like to figure it out by myself for my hw).
Thanks!
so let me introduce the scalar function [tex]\Phi[/tex] = -(x2+y2+z2)(-1/2) which some of you may recognize as minus one over the radial distance from the origin.
When I compute [tex]\nabla[/tex]2[tex]\Phi[/tex] is get 0.
Now if I do the following integral on the surface S of the unit sphere x2+y2+z2= 1 :
[tex]\int[/tex][tex]\int[/tex][tex]\nabla[/tex][tex]\Phi[/tex][tex]\bullet[/tex]n dS
I obtain 4[tex]\pi[/tex] which is just the surface area of the unit sphere since the laplacian of [tex]\Phi[/tex] dotted with the unit radial vector turns out to be one.
Yet the Divergence Theorem
tells me precisely that those two quantities should be equal, but integrating the laplacian of phi would give me zero since the latter quantity is already 0.
Any idea on what I'm doing wrong?
(please only suggestion but do not give me the answer straight away if you think you know it, I'd like to figure it out by myself for my hw).
Thanks!