- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Worked example on a covariant vector transformation
- I
- Thread starter Dyatlov
- Start date
In summary: So, in the ##B## basis in terms of is:To find ##V_1## in the ##B## basis in terms of ##V_i## in ##R^2##:First, it is not a good idea to use superscripts for components of a covector. Simple way to restore these formulas is as follows. Vector's coordinates form the column: ##x=(x^1,\ldots, x^m)^T## and covector's coordinates form the row ##\xi=(\xi_1,\ldots, \xi_m)##. The pairing ##\xi x=\xi_ix^i## is a scalar
Physics news on Phys.org
- #2
- 19,018
- 24,049
You should know, that to download a word document from unknown origin is a big hurdle not many of us want to risk. Definitely not me, as I additionally consider it as bad behavior to force me to take action rather than trying to concentrate on help. But this is my personal attitude towards users who don't take the effort of posting their questions adequately while simultaneously demanding efforts from others. I think you should know this and consider to type in the entire question instead. We have a LaTex library in place that helps a lot to even type in complicated formulas.Dyatlov said:Hello.
I would like to check my understanding of how you transform the covariant coordinates of a vector between two bases.
I worked a simple example in the attached word document.
Let me know what you think.
- #3
jedishrfu
Mentor
- 14,802
- 9,152
- #4
jedishrfu
Mentor
- 14,802
- 9,152
Here's the content of the PDF (limited to 10 image files per post so had to use latex codes for some stuff) via copy and paste (equations are images)
----------------------// example.docx as pdf //----------------------------------------------
The formula for the covariant vector transformation from the ##R^2## coordinate system to the ##B## coordinate system is:
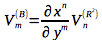
For our example, the vector
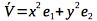 , where
, where
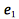 and
and
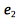 are the basis for
are the basis for
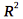 .
.
Our new coordinate system
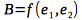 ; spanned by
; spanned by
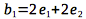
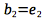
To find ##V_1## in the ##B## basis in terms of ##V_i## in ##R^2##:
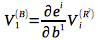
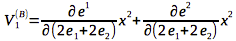
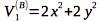
----------------------// example.docx as pdf //----------------------------------------------
The formula for the covariant vector transformation from the ##R^2## coordinate system to the ##B## coordinate system is:
For our example, the vector
Our new coordinate system
To find ##V_1## in the ##B## basis in terms of ##V_i## in ##R^2##:
- #5
zwierz
- 334
- 62
First, it is not a good idea to use superscripts for components of a covector. Simple way to restore these formulas is as follows. Vector's coordinates form the column: ##x=(x^1,\ldots, x^m)^T## and covector's coordinates form the row ##\xi=(\xi_1,\ldots, \xi_m)##. The pairing ##\xi x=\xi_ix^i## is a scalar.
If vector's coordinates transform with the help of a matrix ##C## by the rule ##x'=Cx## and the covector's coordinates transform as follows ##\xi'=\xi D##
then formula ##\xi'x'=\xi x## implies ##D=C^{-1}##
If vector's coordinates transform with the help of a matrix ##C## by the rule ##x'=Cx## and the covector's coordinates transform as follows ##\xi'=\xi D##
then formula ##\xi'x'=\xi x## implies ##D=C^{-1}##
Last edited:
Related to Worked example on a covariant vector transformation
1. What is a covariant vector?
A covariant vector is a mathematical object that represents a physical quantity and transforms in a specific way under coordinate transformations. It is also known as a contravariant vector and is denoted by a superscript index, such as vi.
2. What is the purpose of a worked example on a covariant vector transformation?
The purpose of a worked example on a covariant vector transformation is to demonstrate how a covariant vector changes when the coordinate system is transformed. This helps to understand the concept of covariant vectors and how they behave under different coordinate systems.
3. How is a covariant vector transformed?
A covariant vector is transformed using the chain rule in multivariable calculus. This involves multiplying the vector by a Jacobian matrix, which contains the partial derivatives of the new coordinates with respect to the old coordinates. The result is a new covariant vector in the new coordinate system.
4. What is the difference between a covariant vector and a contravariant vector?
A covariant vector transforms in a specific way under coordinate transformations, while a contravariant vector transforms in the opposite way. This means that their components have different transformation rules, with covariant vectors using the chain rule and contravariant vectors using the inverse of the Jacobian matrix.
5. Why are covariant vectors important in physics?
Covariant vectors are important in physics because they represent physical quantities, such as velocity, momentum, and force, in a way that is independent of the coordinate system. This allows for easier calculations and analysis of physical phenomena, as well as a more intuitive understanding of the underlying mathematical concepts.
Similar threads
-
Differential Geometry
- Replies
- 16
- Views
- 3K
-
Differential Geometry
- Replies
- 11
- Views
- 4K
-
Differential Geometry
- Replies
- 15
- Views
- 4K
-
Differential Geometry
- Replies
- 2
- Views
- 3K
-
Special and General Relativity
- Replies
- 5
- Views
- 1K
-
Advanced Physics Homework Help
- Replies
- 5
- Views
- 2K
-
Differential Geometry
- Replies
- 21
- Views
- 683
-
Differential Geometry
- Replies
- 2
- Views
- 1K
-
Differential Geometry
- Replies
- 1
- Views
- 1K
-
Special and General Relativity
- Replies
- 5
- Views
- 2K
Share: