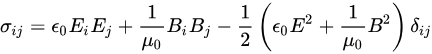anuttarasammyak's latest activity
-
 anuttarasammyak reacted to Klaus3's post in the thread A Conflicting results about Stress tensor symmetry on EM field with
anuttarasammyak reacted to Klaus3's post in the thread A Conflicting results about Stress tensor symmetry on EM field with Like.
This expression for the maxwell stress tensor only works for linear dielectrics or monopolar bodies. It is not necessarily symmetric for...
Like.
This expression for the maxwell stress tensor only works for linear dielectrics or monopolar bodies. It is not necessarily symmetric for... -
 anuttarasammyak replied to the thread A Conflicting results about Stress tensor symmetry on EM field.Explicit expression of Maxwell stress tensor shows obvious symmetry. I do not understand your situation introducing other stress...
anuttarasammyak replied to the thread A Conflicting results about Stress tensor symmetry on EM field.Explicit expression of Maxwell stress tensor shows obvious symmetry. I do not understand your situation introducing other stress... -
 anuttarasammyak replied to the thread B Work done when moving an object.Work done on moving object during short time ##\delta t## is $$\mathbf{F}\cdot\mathbf{v}\delta t$$ During time ##[t_1, t_2]##...
anuttarasammyak replied to the thread B Work done when moving an object.Work done on moving object during short time ##\delta t## is $$\mathbf{F}\cdot\mathbf{v}\delta t$$ During time ##[t_1, t_2]##... -
 anuttarasammyak replied to the thread A Dirac's "comprehensive action principle" -- independent equations.N consists of various fields, e.g., matter, EM field. Each fileld could be independent but there is a constraint that covariant...
anuttarasammyak replied to the thread A Dirac's "comprehensive action principle" -- independent equations.N consists of various fields, e.g., matter, EM field. Each fileld could be independent but there is a constraint that covariant... -
 anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.In [EDIT] of post #6, I tried to get general expression for 2X2 matrix. This expression seems almost unique. Your checks/comments will...
anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.In [EDIT] of post #6, I tried to get general expression for 2X2 matrix. This expression seems almost unique. Your checks/comments will... -
 anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.In my matrix calculation LHS ##\neq## RHS = $$\begin{bmatrix}1&7/2\\1&1\end{bmatrix}$$ which has eigenvalues ##1 \pm \sqrt{\frac{7}{2}}##
anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.In my matrix calculation LHS ##\neq## RHS = $$\begin{bmatrix}1&7/2\\1&1\end{bmatrix}$$ which has eigenvalues ##1 \pm \sqrt{\frac{7}{2}}## -
 anuttarasammyak replied to the thread Calculating the Planck Length.Your estimation would show that we have minimum length, which is order Planck length, for our investigation of space. When we try to...
anuttarasammyak replied to the thread Calculating the Planck Length.Your estimation would show that we have minimum length, which is order Planck length, for our investigation of space. When we try to... -
 anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.In ordet to catch your question exactly, I would like to ask you whether your ##A=P^{-1}DP## setting include...
anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.In ordet to catch your question exactly, I would like to ask you whether your ##A=P^{-1}DP## setting include... -
 anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.I don't think that the diagonalization is possible in general. In the case of normal matrix A, it is.
anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.I don't think that the diagonalization is possible in general. In the case of normal matrix A, it is. -
 anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.As for 2X2 matrices which have eigenvalue l_1 and l_2, their general expression is With parameters ##a_{12} \neq 0## and ##a_{11}##...
anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.As for 2X2 matrices which have eigenvalue l_1 and l_2, their general expression is With parameters ##a_{12} \neq 0## and ##a_{11}##... -
 anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.My bad. I wrongly thought they are real symmetric matrices, or normal matrices.
anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.My bad. I wrongly thought they are real symmetric matrices, or normal matrices. -
 anuttarasammyak reacted to Sciencemaster's post in the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors? with
anuttarasammyak reacted to Sciencemaster's post in the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors? with Like.
Are you sure? I'm pretty sure that ##\begin{bmatrix}1&4\\1&1\end{bmatrix}## has the eigenvectors ##\begin{bmatrix}2\\1\end{bmatrix}##...
Like.
Are you sure? I'm pretty sure that ##\begin{bmatrix}1&4\\1&1\end{bmatrix}## has the eigenvectors ##\begin{bmatrix}2\\1\end{bmatrix}##... -
 anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.For c=2 it is impossible that both the two vectors are eigenvectors. I misinterpreted you mentioned they are eigenvectors...
anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.For c=2 it is impossible that both the two vectors are eigenvectors. I misinterpreted you mentioned they are eigenvectors... -
 anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.In your example the two vectors are orhogonal so -c^2+1=0. Am I misunderstanding you? QDQ^{-1} is a general form of matrix which has...
anuttarasammyak replied to the thread I Can one find a matrix that's 'unique' to a collection of eigenvectors?.In your example the two vectors are orhogonal so -c^2+1=0. Am I misunderstanding you? QDQ^{-1} is a general form of matrix which has... -
 anuttarasammyak replied to the thread A The Lagrangian of a free particle ##L=-m \, ds/dt##.This is also true for SR Lagrangian. For SR Lagrangian pk has the factor \frac{1}{\sqrt{1-v^2/c^2}} as we see in...
anuttarasammyak replied to the thread A The Lagrangian of a free particle ##L=-m \, ds/dt##.This is also true for SR Lagrangian. For SR Lagrangian pk has the factor \frac{1}{\sqrt{1-v^2/c^2}} as we see in...