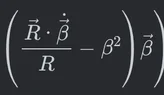anuttarasammyak's latest activity
-
 anuttarasammyak replied to the thread Help with derivation of electric field of a moving charge.The first term has dimension of T^-1 though it should be non dimensional. You should investigate its derivation.
anuttarasammyak replied to the thread Help with derivation of electric field of a moving charge.The first term has dimension of T^-1 though it should be non dimensional. You should investigate its derivation. -
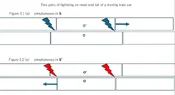
 anuttarasammyak replied to the thread I Relativity of simultaneity in actuality.The author explains the figures saying "the point of view of S(or S′)". Therefore, there is a possibility that readers may...
anuttarasammyak replied to the thread I Relativity of simultaneity in actuality.The author explains the figures saying "the point of view of S(or S′)". Therefore, there is a possibility that readers may... -
 anuttarasammyak replied to the thread A Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature?.I see. “The moving inertial frame against the original IFR” would eliminate those cases.
anuttarasammyak replied to the thread A Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature?.I see. “The moving inertial frame against the original IFR” would eliminate those cases. -
 anuttarasammyak reacted to wrobel's post in the thread A Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature? with
anuttarasammyak reacted to wrobel's post in the thread A Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature? with Like.
I was hoping that the name existed. :( The moving frame can for example rotate and its different points can have different velocities...
Like.
I was hoping that the name existed. :( The moving frame can for example rotate and its different points can have different velocities... -
 anuttarasammyak replied to the thread A Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature?.I do not think so. In the text, "(absolute) velocity of the moving frame" is better.
anuttarasammyak replied to the thread A Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature?.I do not think so. In the text, "(absolute) velocity of the moving frame" is better. -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.An example of my point. Say light is passing on element ##dx^\mu##, i.e., $$ g_{\mu\nu}dx^\mu dx^\nu = 0 $$ After variation of metric $$...
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.An example of my point. Say light is passing on element ##dx^\mu##, i.e., $$ g_{\mu\nu}dx^\mu dx^\nu = 0 $$ After variation of metric $$... -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.Yes. For $$g_{\mu\nu}= g_{\mu\alpha} g_{\beta\nu} g^{\alpha\beta},\ g^{\mu\alpha} g_{\alpha\nu}=\delta^\mu_\nu...
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.Yes. For $$g_{\mu\nu}= g_{\mu\alpha} g_{\beta\nu} g^{\alpha\beta},\ g^{\mu\alpha} g_{\alpha\nu}=\delta^\mu_\nu... -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.$$\bar{g}_{\mu\nu} - g_{\mu\nu} = \delta g _{\mu\nu} = - \delta \bar{g}_{\mu\nu} $$ ##\bar{g}_{\mu\nu}## is a tensor in the world where...
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.$$\bar{g}_{\mu\nu} - g_{\mu\nu} = \delta g _{\mu\nu} = - \delta \bar{g}_{\mu\nu} $$ ##\bar{g}_{\mu\nu}## is a tensor in the world where... -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.I agree that index raise- lower operation should be done using one same, old or new, metric for all the indexes of all the entities in...
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.I agree that index raise- lower operation should be done using one same, old or new, metric for all the indexes of all the entities in... -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.My bad. I withdraw it.
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.My bad. I withdraw it. -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.To me the point is two metrics: original and varied. In varied metric world what kind of things or relations remain and what does not ?
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.To me the point is two metrics: original and varied. In varied metric world what kind of things or relations remain and what does not ? -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.Thanks. I will restate it to confirm my understanding. Here I try not to refer controversial (at least to me) tensor and concentrate on...
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.Thanks. I will restate it to confirm my understanding. Here I try not to refer controversial (at least to me) tensor and concentrate on... -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.First of all, thanks @JimWhoKnew So in general cases which could include ##\delta g^{\mu\nu}##, do we need further information or...
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.First of all, thanks @JimWhoKnew So in general cases which could include ##\delta g^{\mu\nu}##, do we need further information or... -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.I am sorry I don't understand "the same signature". If A is g itself, I think that B = A = g. A=mg, B=1/m g where m is a real number...
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.I am sorry I don't understand "the same signature". If A is g itself, I think that B = A = g. A=mg, B=1/m g where m is a real number... -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.Going back to basics, Dirac's textbook defines a tensor as follows: $$...
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.Going back to basics, Dirac's textbook defines a tensor as follows: $$...