Recent content by qft-El
-
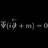
Graduate Solving renormalization group equation in QFT
I've put some thoughts and here's what I'll flesh out what I think is going on. I would appreciate to have feedback if you think this is flawed or not. To avoid confusion with the notation, I'll switch the notation from ##\lambda\to u## for the parameter. Furthermore, I'll use the ##_R##...- qft-El
- Post #6
- Forum: Quantum Physics
-
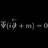
Graduate Solving renormalization group equation in QFT
I know it may not be relevant to the question, but here's a summary of how I've found this book. I was reading a brief section about the RG equation and Callan-Symanzik equation on an introductory QFT book: A Modern Introduction to Quantum Field Theory by Michele Maggiore and I found this...- qft-El
- Post #5
- Forum: Quantum Physics
-
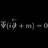
Graduate Solving renormalization group equation in QFT
Hello, vanshees71. I'm glad to receive your feedback. I happened to check your notes a couple of days ago, by the way. I think it was some other doubt related to renormalization. Regarding the section that you mention, I see that you solve the homogenous RGE there and it also appears to be more...- qft-El
- Post #3
- Forum: Quantum Physics
-
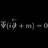
Graduate Solving renormalization group equation in QFT
I'm learning about the RG equation and Callan-Symanzik equation. In ref.1 they claim to solve the RG equation via the method of characteristics for PDE. Here's a picture of the relevant part: First, the part I don't understand - the one underlined in red. What does "compatible" mean here...- qft-El
- Thread
- Partial differential equations Quantum field theory Renormalization Renormalization group
- Replies: 5
- Forum: Quantum Physics
-
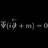
Graduate In what representation do Dirac adjoint spinors lie?
I hope this is the right section as the question is about Lie groups and representations. First and foremost, in this post I'll be dealing with Dirac and Weyl spinor (not spinor fields) representations of the Lorentz algebra. Also, for simplicity, I'll use the chiral representation later on...- qft-El
- Thread
- Lorentz group Representation theory Spinors
- Replies: 1
- Forum: Differential Geometry
-
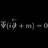
Graduate Heisenberg picture and Path integrals (Zee QFT)
Oh, I have those notes, there is also a free version on arXiv if I recall correctly. Since you take out the topic, the books I use are: A Modern Introduction to Quantum Field Theory, Michele Maggiore. An Introduction to Quantum Field Theory, Peskin&Schroeder The Quantum Theory of Fields...- qft-El
- Post #14
- Forum: Quantum Physics
-
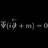
Graduate Heisenberg picture and Path integrals (Zee QFT)
Regarding the book itself, I attached the pages of the book in the spoiler at the end of the first post, so you can check that's exactly what it's written there. Yes, that's my point. The only thing that bugs me now is: which makes the author's point even more mysterious!- qft-El
- Post #12
- Forum: Quantum Physics
-
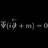
Graduate Heisenberg picture and Path integrals (Zee QFT)
To be honest what really puzzles me is that I checked the previous edition and it turns out this remark was added in the latest one...- qft-El
- Post #9
- Forum: Quantum Physics
-
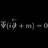
Graduate Heisenberg picture and Path integrals (Zee QFT)
Yes. "Heisenberg/Schrödinger picture completeness relations" were a shorthand for "completeness relations respectively of eigenstates of instantaneous position operator in Heisenberg picture or eigenstates of position operator in Schrödinger picture." The distinction between the two pictures...- qft-El
- Post #6
- Forum: Quantum Physics
-
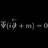
Graduate Heisenberg picture and Path integrals (Zee QFT)
According to Modern Quantum Mechanics by J.J. Sakurai and Napolitano, what you have written is the Heisenberg completeness relation. Furthermore, in Heisenberg picture the position operator is time dependent, as you said. Its eigenstates are different at each instant and fixing time they...- qft-El
- Post #4
- Forum: Quantum Physics
-
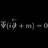
Graduate Heisenberg picture and Path integrals (Zee QFT)
Reading the introduction to path integrals given in the latest edition of Zee's "Quantum field theory in a nutshell", I have found a remark which I don't really understand. The author is evaluating the free particle propagator ##K(q_f, t; q_i, 0)## $$\langle q_f\lvert e^{-iHt}\lvert q_i...- qft-El
- Thread
- Heisenberg heisenberg picture Integrals Path Path integrals Picture Qft
- Replies: 15
- Forum: Quantum Physics
-
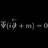
What should a Physics student know before joining a scientific community?
Hello there! I'm a Physics student. I don't know what else I should say (or I feel like saying) about myself. I'm glad to join this community and hopefully enjoy my time here!- qft-El
- Thread
- Intro and greeting
- Replies: 1
- Forum: New Member Introductions