DaveC426913
Gold Member
2025 Award
- 24,353
- 8,563
- TL;DR
- How can I calculate - or better yet visualize - where on the compass the sun will rise and set?
One piece of Earth/astro geometry that always confused me is why the sun is able to set north of West. (I suppose it must also rise north of East, but I'll have to take the word of Early Birds on that.)
I try to build a mental model of the Earth's tilt over the seasons and visualize where the Sun should appear but I can never quite construct the 3D geometry.
For a latitude of, say, 45°N, how can I calculate (or better yet, diagram) sunset and sunrise bearings (0-360°) or compass points over the course of the year? If I know its October, I should be able to look toward the sun on the horizon and say with confidence "that's bearing X".
(I know of several confounding factors, which I can account for under field conditions, once I know the data:
Basically, it'll be an annalemma, flattened onto the horizon (but including compass marks and/or bearings).
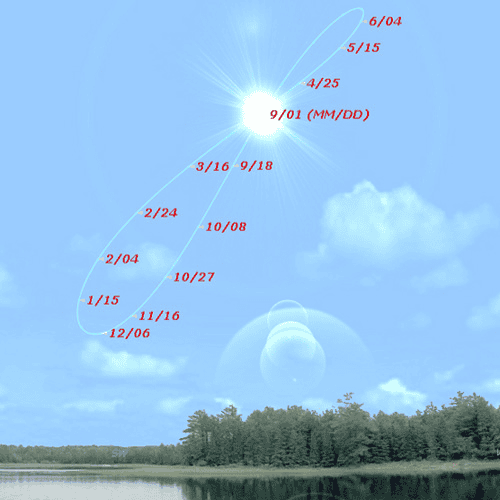
So, instead of the time of sampling being the constant (usually noon, as on a standard annalemma), this would have altitude (0°) constant, letting the time vary.
I try to build a mental model of the Earth's tilt over the seasons and visualize where the Sun should appear but I can never quite construct the 3D geometry.
For a latitude of, say, 45°N, how can I calculate (or better yet, diagram) sunset and sunrise bearings (0-360°) or compass points over the course of the year? If I know its October, I should be able to look toward the sun on the horizon and say with confidence "that's bearing X".
(I know of several confounding factors, which I can account for under field conditions, once I know the data:
- the sun rises and sets at an oblique-r angle in the winter-er months, meaning the margin of error can become embiggened.
- the rate of change in position changes over the season, being quite slow near the equinoxen and quite fast near the solsteese.)
Basically, it'll be an annalemma, flattened onto the horizon (but including compass marks and/or bearings).
So, instead of the time of sampling being the constant (usually noon, as on a standard annalemma), this would have altitude (0°) constant, letting the time vary.
Last edited:



