I_Try_Math
- 119
- 25
- Homework Statement
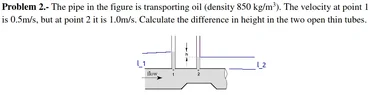
- The pipe in the figure is transporting oil (density 850 kg/m3). The velocity at point 1
is 0.5m/s, but at point 2 it is 1.0m/s. Calculate the difference in height in the two open thin tubes
- Relevant Equations
- Bernoulli's equation
Trying to find an equation for the pressure difference between point 1 and 2. Not sure if my overall reasoning is incorrect, or I introduced a sign error somehow. The equation I come up with implies that the difference is a negative number, but that can't be true if the area of pipe at point 1 is larger than it is at point 2, as it in the given diagram?
Here's my work:
## l_1 ## and ## l_2 ## are intended to mean the distance from points 1 and 2 to where the fluid meets the air.
## P_1 + \rho g l_1 = P_{atm} ##
## P_2 + \rho g l_2 = P_{atm} ##
## P_1 + \rho g l_1 = P_2 + \rho g l_2 ##
## P_1 - P_2 + \rho g l_1 = \rho g l_2 ##
## P_1 - P_2 = \rho g l_2 - \rho g l_1 ##
## P_1 - P_2 = \rho g(l_2 - l_1) ##
## P_1 - P_2 = \rho g(-h) ##
Here's my work:
## l_1 ## and ## l_2 ## are intended to mean the distance from points 1 and 2 to where the fluid meets the air.
## P_1 + \rho g l_1 = P_{atm} ##
## P_2 + \rho g l_2 = P_{atm} ##
## P_1 + \rho g l_1 = P_2 + \rho g l_2 ##
## P_1 - P_2 + \rho g l_1 = \rho g l_2 ##
## P_1 - P_2 = \rho g l_2 - \rho g l_1 ##
## P_1 - P_2 = \rho g(l_2 - l_1) ##
## P_1 - P_2 = \rho g(-h) ##